
« Brachistochrone » : voilà un bien drôle de nom pour une courbe ! C’est pourtant beaucoup plus qu’un simple objet géométrique, c’est la solution à un problème d’optimisation qui a tenu en haleine les mathématiciens du XVII e siècle, même les plus aguerris, et qui a essaimé dans d’autres domaines pour donner finalement naissance au calcul des variations.
Chemin le plus rapide : les débuts
Le problème, au départ, s’est posé en termes simples : trouver la ligne droite que peut décrire le plus vite possible un point partant de A pour aller en B, situé sur une verticale. Il s’agit là du problème de la droite brachistochrone (composé de deux mots grecs signifiant « le plus court » et « le temps »).
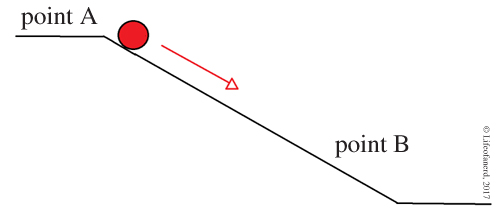
La solution est venue de Galilée qui, en 1638, dans son Discours sur deux nouvelles sciences (la mécanique ou l’étude du mouvement, et la résistance des matériaux), a calculé qu’une telle ligne devait faire avec la verticale un angle de 45°. Il calcule ensuite que si le point pesant se déplace de A vers B en utilisant des lignes droites, il atteindra B plus rapidement en naviguant le long des segments [AC] puis [BC], où C est élément d’un ... Lire la suite
