
Si l’on vous donne une suite qui commence par 2, 4, 132, 2 192, 16 390, 78 132, 279 944,
823 552, 2 097 162, 4 782 980, comment faire pour trouver le terme suivant ? L’astuce est de faire la différence entre deux termes successifs. Puis de recommencer avec les nouveaux nombres obtenus. On s’arrête dès que la ligne ne contient qu’un terme unique (ici, c’est la ligne 7, qui ne contient que le terme 5 040). On en déduit que l’on a affaire aux valeurs prises par un polynôme de degré 7.
Maintenant, comment trouver le terme suivant ?
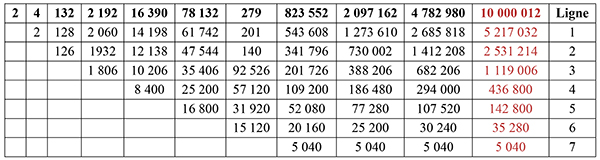
Chaque terme est obtenu en faisant la différence entre le terme
directement au-dessus et celui au-dessus à gauche.
La colonne en rouge se remplit de bas en haut, en partant
de 5 040, jusqu’à l’obtention du nombre cherché, 10 000 012.
Simplement en propageant les différences :
35 280 = 30 240 + 5 040,
puis 142 800 = 107 520 + 35 280,
ensuite 436 800 = 294 000 + 142 800,
on en déduit 1 119 006 = 682 206 + 436 800,
suivi deLire la suite
