
Vous possédez une centrale de production électrique et vous souhaitez transporter l’électricité vers un consommateur. Pour cela, vous allez utiliser le réseau constitué de lignes électriques qui passent par des répartiteurs. Chaque ligne ne peut transférer qu’un débit limité de courant, correspondant à l’intensité maximale qu’elle peut supporter. Vous cherchez à acheminer le maximum d’électricité entre la centrale de production et le client, tout en respectant les capacités des lignes électriques. Comment procéder ?
Un graphe pour modéliser le réseau électrique
Ce problème va être modélisé à l’aide de la théorie des graphes. Les arcs représentent les lignes électriques avec un sens de circulation du courant, et les sommets (ou nœuds) modélisent les répartiteurs, la centrale et le client (voir la figure ci-dessous).
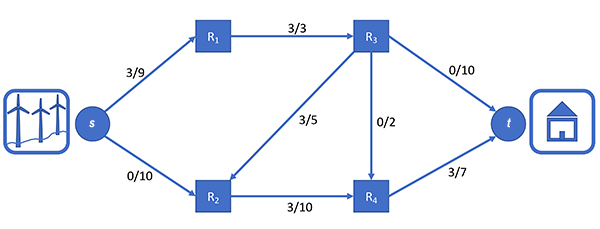
Sur chaque arc, on écrit valeur du flot / capacité de l’arc. Par exemple,
pour l’arc de s à R 1 , le flot a une valeur de 3 et une capacité de 9.
Ce graphe comporte deux sommets particuliers : la centrale est le sommet appelé source s, où le courant ne fait que sortir, et le client est le sommet appelé puits t, où le courant ne fait qu’entrer. Le reste des sommets, les répartiteurs, sont connectés à des ... Lire la suite
