Découvert et démontré en 1898 par le mathématicien britannique Frank Morley (1860‒1937) devenu professeur d’université aux États-Unis, le théorème qui porte le nom de son inventeur et a fait sa célébrité est d’apparence anodine :
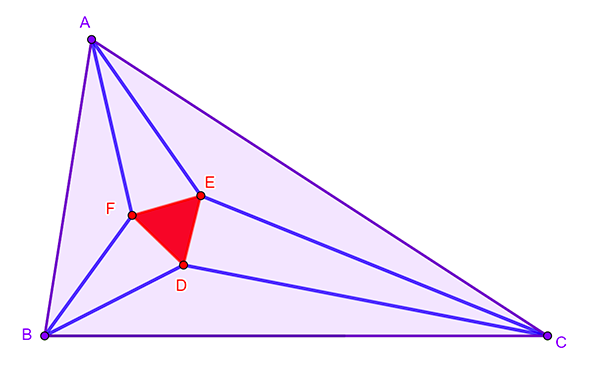
Les points d’intersection des trisectrices adjacentes des angles d’un triangle quelconque ABC sont les sommets d’un triangle équilatéral DEF.
D’un triangle quelconque, on peut donc faire jaillir un triangle équilatéral : c’est la surprise de ce résultat, maintes fois démontré par diverses méthodes géométriques ou trigonométriques et qui garde cependant son côté merveilleux.
En rouge, le triangle de Morley.
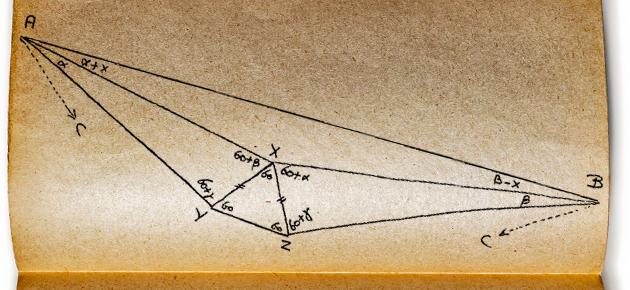
Frank Morley a, semble-t-il, obtenu ce théorème comme conséquence de ses recherches sur la cardioïde, au cours desquelles il a rencontré un lieu géométrique constitué de neuf droites. Si la preuve de Morley lui-même n’était pas simple, d’innombrables autres démonstrations, dont certaines sont relativement élémentaires, ont circulé depuis que ce théorème devenu célèbre a été énoncé. On en a même rencontré quelques-unes qui sont fausses ! Les plus connues des preuves correctes sont celles données en 1922 par l’ingénieur mathématicien français Raoul Bricard (exclusivement géométrique), en 1932 par le mathématicien belge André Letac (qui animait la revue Sphinx), ou en 1962 par le dentiste ... Lire la suite