

Reconnaissez-vous les personnes représentées sur cette figure ? Normalement non, car ces personnes… n’existent pas ! Ces portraits ont été générés automatiquement par un code informatique (un réseau de neurones), qui a été entraîné pour pouvoir créer autant de portraits que l’on souhaite. Un des outils utilisés pour entraîner ce réseau de neurones est le transport optimal. Cette théorie mathématique, qui date d’il y a plus de deux siècles, s’avère en effet très utile dans le domaine en pleine ascension de la science des données. La physique, l’économie ou le traitement d’image font également appel au transport optimal pour résoudre leurs problématiques.
Monge, un précurseur
L’histoire du transport optimal commence avec le mathématicien français Gaspard Monge. Né à Beaune (Côte-d’Or), il se fait remarquer à 17 ans en dessinant un plan détaillé de sa ville natale. Il y montre une réelle vocation pour la géométrie. Il est alors engagé comme assistant à l’École royale du génie de Mézières (Ardennes), étant d’origine trop modeste pour y être admis comme élève. Il devient rapidement professeur de mathématiques et de physique. Il va y enseigner pendant presque vingt ans, et avoir en parallèle une activité scientifique foisonnante et variée, dans laquelle son enseignement, sa recherche, et les applications sont intimement mêlés.

Les activités scientifiques de Monge se nourrissent d’applications, souvent inspirées de questions militaires. En 1781, il présente à l’Académie des sciences son Mémoire sur la théorie des déblais et des remblais. La question à laquelle il tente de répondre est : comment déplacer un tas de sable qui a une certaine forme (le déblai), pour le transformer en un autre tas de sable (le remblai) à un autre endroit, de même volume et de forme prescrite, et cela en rendant minimale la somme des distances parcourues par les grains de sable ?

Gaspard Monge, conte de Péluse (1746 — 1818), gravure de Naigeon Jeune.
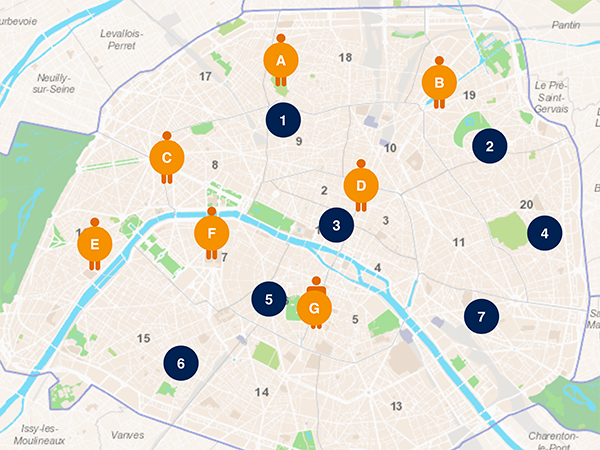
Voyons une instance du problème. On suppose que N individus d’une même ville (représentés ici par des lettres capitales A, B… G) souhaitent tous lire le même livre, et que N bibliothèques de la ville (représentées par des chiffres) possèdent chacune un exemplaire de ce livre. On se demande comment ces N personnes doivent se répartir pour que chacune d’elles aille chercher un exemplaire dans une bibliothèque, sans créer de conflit (chaque bibliothèque ne reçoit qu’une seule de ces personnes puisqu’elle ne possède qu’un exemplaire du livre), et de manière que la somme des distances parcourues soit minimale. Cette question s’appelle le problème del’appariement optimal.
Pour le résoudre, on peut construire un tableau contenant les distances entre les personnes et les bibliothèques. Les colonnes correspondent aux individus, et les lignes aux bibliothèques. Résoudre le problème revient à colorier N cases, de telle manière qu’une seule case par colonne et une seule case par ligne soit coloriée (pas de conflit), et que la somme des distances sur les cases coloriées soit la plus faible possible.
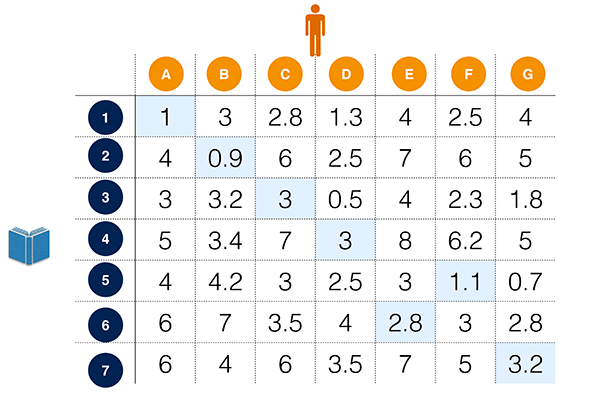
Tableau des distances (en km) entre les individus et les bibliothèques.
En bleu, la solution du problème d’appariement.
Plutôt que prendre les distances entre les points, on aurait pu prendre le temps de trajet à vélo, ou toute autre fonction de coût entre les personnes et les bibliothèques, ce qui aurait abouti à un tableau différent, et donc à un résultat différent (voir encadré).
Résoudre le problème d’appariement
Comment faire en pratique pour trouver la solution ? Le nombre de coloriages du tableau satisfaisant la contrainte (une seule case coloriée par colonne, et une seule case coloriée par ligne) est égal à N! = N × (N-1) ×… × 1, car on commence par choisir la case coloriée dans la première colonne (N choix), puis dans la deuxième (N-1 choix car une ligne est exclue), et ainsi de suite.
La quantité N! (factorielle de N) est « raisonnable » pour l’exemple que l’on a pris ici
(7! = 5040), mais elle devient vite gigantesque. Par exemple, 100! est de l’ordre de 10158. Il est donc très vite impossible d’énumérer toutes les solutions pour trouver la plus économique. Des algorithmes d’optimisation combinatoire dédiés à résoudre ce problème d’appariement existent, comme l’algorithme hongrois, aussi appelé algorithme de Kuhn-Munkres.
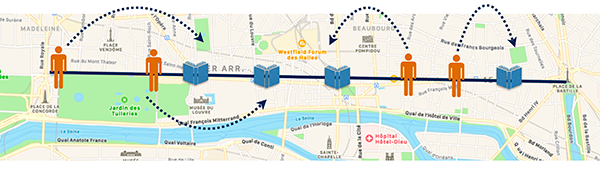
Il existe un cas particulier dans lequel on sait facilement trouver une solution au problème d’appariement : celui où toute les bibliothèques et les individus se trouvent sur une même droite. Le problème est alors à une dimension. Si la fonction de coût pour se déplacer est la distance, ou le carré de la distance, alors une solution au problème est donnée par le réarrangement monotone : on ordonne les bibliothèques et les individus de gauche à droite sur la ligne, et on envoie le premier individu sur la première bibliothèque, et ainsi de suite. La solution trouvée n’est pas forcément unique (plusieurs solutions distinctes peuvent correspondre au minimum de la fonction coût).
Le problème d’appariement de points a une application très amusante en traitement d’image : il permet de transférer les couleurs d’une image à une autre. Une image est un tableau rectangulaire dont chaque case (pixel) contient trois valeurs encodant une couleur (voir Mathématiques et Imagerie, hors-série 77, 2021). Ces trois valeurs correspondent à des coordonnées de rouge, vert et bleu dans un espace colorimétrique de trois dimensions. En appariant les couleurs de deux images par transport optimal, on peut transformer chaque couleur de la première en sa couleur correspondante dans la seconde. Ce processus est appelé transfert de couleur et est utile notamment en post-production vidéo.
En haut, deux prises de vue non retouchées à Cherbourg-en-Cotentin (Manche).
Ci-dessus, expérience de transfert de couleur : la première prise de vue a reçu les couleurs de la seconde prise de vue.
Les routes du sable
Revenons à Monge. Le problème qui l’intéresse est plus général que celui des bibliothèques. On doit envoyer un tas de sable de forme donnée, vers un autre de forme également prescrite. On doit toujours rendre minimale la somme des distances parcourues par les grains de sables, sous la contrainte que les grains sont distribués selon le déblai au départ et le remblai à l’arrivée. Monge ne résout pas son problème, mais il part du principe que la solution existe, et cherche quelles propriétés géométriques elle peut vérifier.
Il étudie le problème en deux dimensions, puis en trois. Il montre notamment que les routes ne se coupent pas : si l’on doit envoyer deux grains de sables des points A, B vers les points a, b, alors les routes qui permettent de rendre minimale la somme des déplacements ne peuvent pas se couper (voir encadré).
Les routes ne se coupent pas !
Dans son manuscrit, Monge explique que les routes empruntées par les grains de sable ne se coupent pas entre leurs extrémités si le coût pour apparier deux points est la distance entre ces points. Prenons deux grains de sable positionnés aux points A et B, que l’on souhaite envoyer sur les points a et b. On se demande s’il vaut mieux envoyer le grain positionné en A vers a (et donc le grain en B vers b) ou l’inverse.
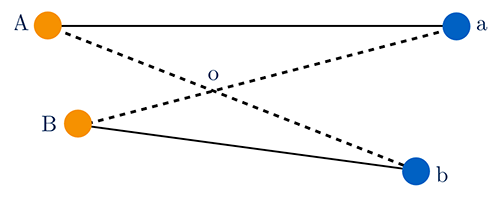
Or, l’inégalité triangulaire nous dit que Aa ≤ Ao + oa et que Bb ≤ Bo + ob. Comme la somme des longueurs des routes en pointillés est égale à Ab + Ba, soit Ao + oa + Bo + ob, on en déduit que Aa + Bb est inférieure à Ab + Ba. Ainsi, la somme des longueurs des routes en trait plein est inférieure à la somme des longueurs des routes en pointillés.
Le problème de Monge est en réalité particulier et difficile. On peut construire des exemples simples où il n’a pas de solution unique mais plusieurs solutions, et d’autres où il n’y a tout simplement pas de solution. Un siècle plus tard (à la fin du XIXe siècle donc), la question n’est toujours pas résolue et l’Académie des sciences la propose à l’occasion du prix Bordin.
Il faut attendre le XXe siècle pour que la question de l’existence de solutions au problème du transport optimal soit enfin résolue. D’importantes avancées sont proposées par plusieurs mathématiciens dès les années 1930 et pendant la Seconde Guerre mondiale, notamment pour répondre à des questions d’allocation de ressources et d’optimisation de production en économie. Toutes ces idées émergent en parallèle et indépendamment chez plusieurs scientifiques, aussi bien « à l’ouest » qu’« à l’est ».
Kantorovitch entre en scène
Les contributions les plus importantes sur le sujet sont apportées par le mathématicien russe Leonid Vitalievitch Kantorovitch (1912-1986). Il développe les outils de la programmation linéaire, l’une des contributions les plus significatives à la théorie économique du XXe siècle. Il va recevoir le prix Nobel d’économie en 1975 avec Tjalling Charles Koopmans (1910-1985) pour ces travaux.
Le problème étudié par Kantorovich est légèrement différent de celui de Monge. Revenons à nos individus et bibliothèques. Dans le problème de Monge, on a autant de personnes que de bibliothèques et on cherche à les apparier. Dans la version de Kantorovich, chaque bibliothèque peut posséder plusieurs exemplaires du livre, et chaque personne est remplacée par un foyer de plusieurs individus vivant au même endroit et souhaitant lire l’ouvrage tant convoité.
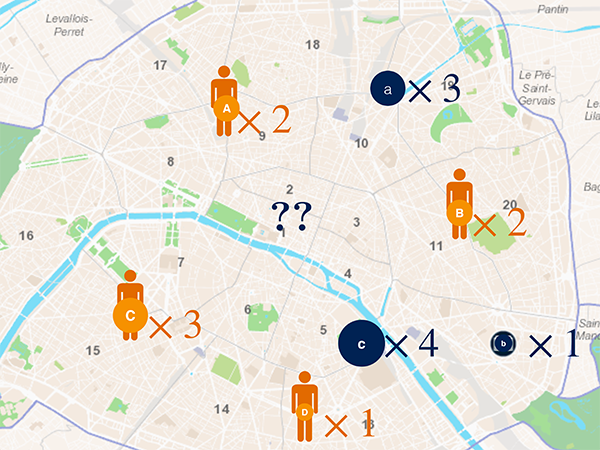
La somme totale des individus souhaitant lire le livre dans tous les foyers est égale à la somme totale des exemplaires dans toutes les bibliothèques. On souhaite toujours trouver comment répartir les individus dans les différentes bibliothèques de manière qu’il n’y ait pas de conflit et que tous les individus soient satisfaits, en minimisant la somme des déplacements. Mais cette fois-ci, plusieurs individus d’un même foyer peuvent se répartir vers des bibliothèques différentes (et inversement, une même bibliothèque peut recevoir des individus venant de foyers différents).
Pour résoudre le problème de Kantorovich, on crée à nouveau une matrice de distances entres les foyers (A, B, C et D) et les bibliothèques (a, b et c). On écrit caA la distance entre le foyer A et la bibliothèque a, et ainsi de suite. Puis on crée un autre tableau de même taille, qui indique comment les différents foyers se répartissent entre les bibliothèques. La valeur paA par exemple désigne combien d’individus du foyer A vont aller à la bibliothèque a.
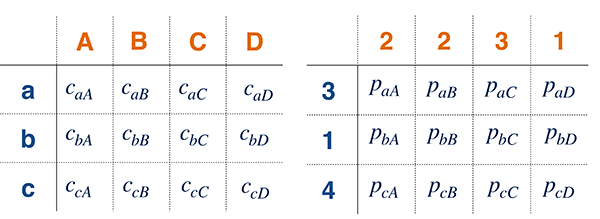
Les valeurs de ce tableau doivent vérifier des contraintes : le nombre d’individus des différents foyers qui vont à la bibliothèque a doit être exactement égal au nombre d’exemplaires du livre dans cette bibliothèque (c’est-à-dire 3). De même, le nombre d’individus visitant les bibliothèques depuis le foyer A doit être exactement égal au nombre d’individus de ce foyer (soit 2). Toutes ces contraintes se traduisent par sept équations, fixant les sommes des valeurs du tableau sur chaque ligne et sur chaque colonne. 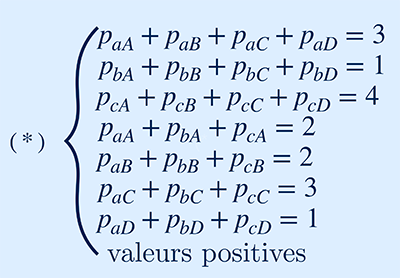
On cherche ensuite à remplir le tableau de manière à rendre la somme des produits entre les pi,j et les coûts ci,j minimale sous la contrainte que les quantités p sont positives et vérifient les sept équations, c’est-à-dire :
Le problème obtenu est un cas particulier d’une classe de problèmes plus généraux dits de programmation linéaire. Un algorithme très connu pour les résoudre est celui du simplexe, dû à George Dantzig en 1947 (voir la Recherche opérationnelle, hors-série 75, 2020).
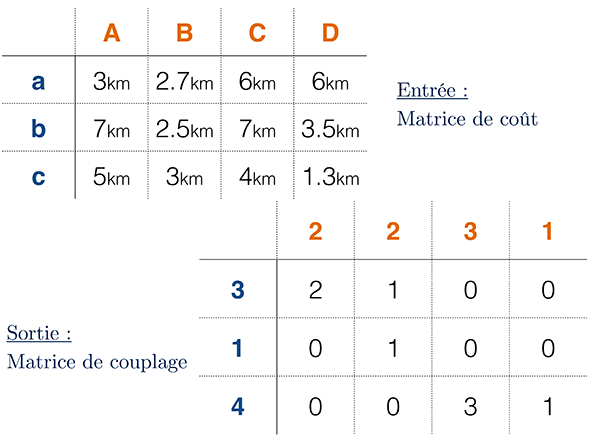
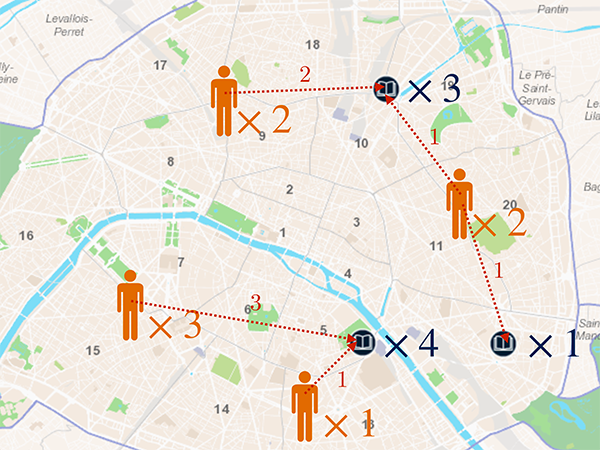
Solution du problème de transport optimal de Kantorovich.
Un outil clef
Il faut attendre les années 1990 et les travaux du mathématicien français Yann Brenier notamment pour que soient explicitées les conditions sous lesquelles les solutions du problème de Kantorovitch fournissent des solutions au problème de Monge. Depuis, l’école franco-italienne du transport optimal s’est considérablement développée et a connu de nombreux succès, aussi bien du côté des mathématiques théoriques que des mathématiques appliquées. Le transport optimal est également devenu un outil clef dans de nombreux champs applicatifs, comme l’économie, l’informatique graphique ou encore la physique. Le transport optimal a par exemple des liens forts avec la mécanique des fluides. En imagerie, il est impliqué pour modifier le contraste ou la couleur dans les images, pour comparer ou créer des interpolations entres des formes, manipuler des images de textures… En apprentissage machine, il est devenu un outil incontournable de comparaison de données, notamment utilisé pour entraîner certains réseaux de neurones. Aujourd’hui, le transport optimal fait des merveilles !
Ce texte est issu de la conférence « Des tas de sable aux pixels, deux siècles et demi de transport optimal » donnée par l’auteure le 20 janvier 2021 dans le cadre du cycle « Un texte, un mathématicien » à la Bibliothèque nationale de France.
Julie Delon est professeure de mathématiques et membre du laboratoire de mathématiques appliquées MAP5.

