Les amateurs de mathématiques, et les mathématiciens eux-mêmes, ne sont pas en manque d’imagination ! À partir du nombre d’or, certains ont défini une famille de nombres, les nombres métalliques, possédant certaines propriétés similaires au nombre d’or.

 

Pour n entier vérifiant n ≥ 1, le nombre métallique d’ordre n est la solution positive de l’équation polynomiale du second degré x 2 − n x − 1 = 0.

Pour les premières valeurs de n , on obtient le tableau suivant où, pour n = 1, on retrouve le nombre d’or :

 

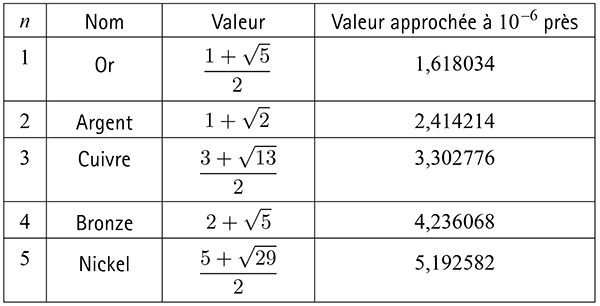
Ces nombres métalliques, que l’on notera ici M n , pour n ≥ 1, peuvent aussi s’exprimer facilement sous forme de fractions continues. 

À partir de l’égalité M n2 − n M n − 1 = 0, on obtient, en passant certains termes dans le second membre  et en divisant par M n : 

De là, on tire l’écriture de Mn en fraction continue :

qui se note alors Mn = [n, n, n, n, n, n, n…].

Du côté des formules avec des radicaux imbriqués, ce n’est guère plus alambiqué. De l’égalité Mn2 - n Mn - 1 = 0, on tire Mn2 = 1 + n Mn puis, en prenant la racine carrée, on obtient  d’où cette nouvelle écriture de Mn :

Bien sûr, toutes ces formules se démontrent de manière rigoureuse.

Lire la suite gratuitement