

La fille d’Éric Trouillot, inventeur du jeu à succès Mathador
et grand ami de la rédaction, s’est illustrée !
Un millésime qui tourne rond
En 2022, le chiffre 2 sera à l’honneur, c’est certain.
Mais 2 + 0 + 2 + 2 = 6 (soit 3×2 = 6) aussi, nous dit le mathémagicien Dominique Souder. Sur la figure qu’il a confectionnée, les douze valeurs inscrites aux intersections sont les termes d’une suite arithmétique de raison 2, à partir de 326.
Sur chacun des cercles situés dans les quatre directions, additionnons les six valeurs rencontrées… et que trouve-t-on ?
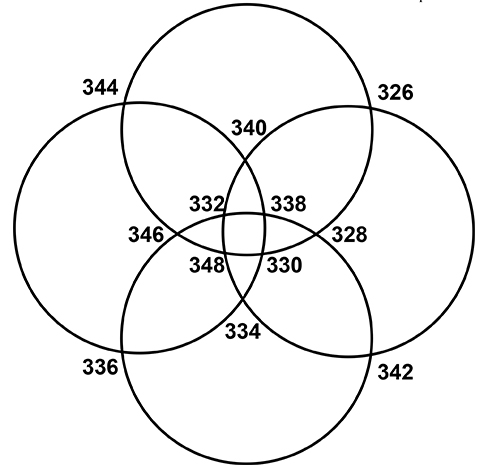
Avec des entiers consécutifs
Dans la rubrique « Affaire de Logique » du quotidien Le Monde, les auteurs, Élisabeth Busser, Gilles Cohen et Jean-Louis Legrand n’ont pas failli à la tradition en proposant par exemple d’écrire 2022 comme somme d’entiers consécutifs :
2 022 = 673 + 674 + 675, ou 2 022 = 504 + 505 + 506 + 507, ou encore 2 022 = 163 + 164 + … + 173 + 174.
Pour trouver de telles sommes, on remarque que la somme des entiers de A à B est celle des entiers de 1 à B moins celle des entiers de 1 à A – 1. Ici, cela conduit à égalité qui conduit à 4 044 = (B+A)(B–A+1). On écrit alors 4 044 comme produit de deux entiers ; les seuls convenables sont 3×1 348, 4×1 011 ou 12×337.
On en déduit, par exemple, que 2 022 = 3×(1 348/2), soit 3×674,
soit encore 673 + 674 + 675.
Avec des chiffres consécutifs cette fois, on peut aussi écrire 2 022 en s’essayant avec le moins de chiffres possibles (en excluant donc 0 au début). Sans utiliser d’autres signes que + ou – , on trouve 2 022 = 1 234 + 5 – 6 +789. Avec tous les signes opératoires sauf la factorielle, et en utilisant de plus en plus de chiffres, on peut proposer :
2 022 = (1–2+3)×(45–6–7), ou (1+2)(3+4) – (5+6)×(7+8), ou encore 1 + 2 + 3 + (4×(56+7)×8), ou enfin, avec les neuf chiffres, (1 + 2 + 3)×((4 – 5 + 6×7)×8 + 9).
Avec tous les signes, y compris la factorielle, François Lavallou et Alain Zalmanski, tous deux champions dans ce domaine, ont trouvé :
2 022 = –1 + 2 + (3!)4 + 5 + 6!,
ou encore (1 + 2)!!×3 – 4! – 5! + 6,
ou enfin 1 + 2 + 3 – 4!×(5!+6) + 7!.
Enfin, pour rester dans l’arithmétique, le mentaliste Benoît Rosemont a confectionné le carré magique suivant, dont les innombrables propriétés ne vous échapperont pas (celles relatives au carré magique de 2021 ont été passées au crible par René Descombes, voir Tangente 202, page 2 ; n’hésitez pas à vous en inspirer !).
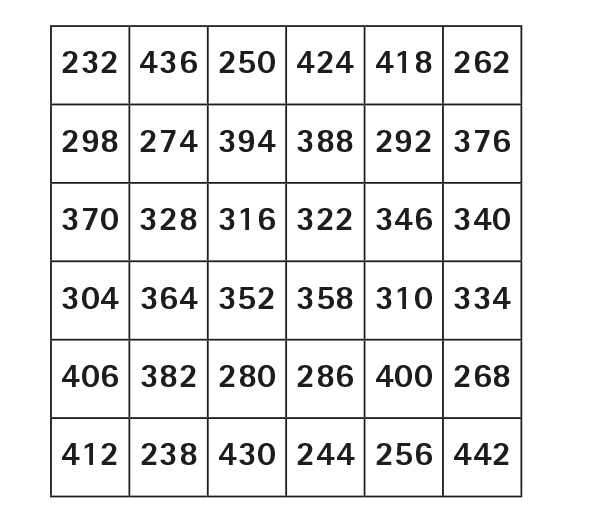
Plus insolite encore
Le nouveau millésime, produit de 2, 3 et 337, a encore de multiples propriétés, qui n’ont pas échappé à nos collègues et amis. Il a été signalé, par exemple, que le carré du « retourné » de 2 022 est aussi le « retourné » de son carré (autrement dit, 2 0222, soit 4 088 484, est le « retourné » de 2 2022, carré qui lui vaut 4 848 804). Mais c’était aussi vrai pour 2 021… et ce ne le sera plus pour 2 023.
2 022 n’est certes pas palindrome… dans notre système décimal. Mais c’est le cas en base 18 (où il s’écrit 646) et en base 43 (où il devient 141), nous dit encore Alain Zalmanski, grand amateur de palindromes.
Pour finir en beauté, Michel Criton nous apprend même que 2 022 est le premier élément d’une suite de quatre nombres de Harshad (nombres divisibles par la somme de leurs chiffres) consécutifs.
En effet, 2 022 = (2 + 2 + 2)×337, 2 023 = (2 + 2 + 3)×289, 2 024 = (2 + 2 + 4)×253, 2 025 = (2 + 2 + 5)×225. Joli !
