La notion de puissance définie par rapport à un cercle amène naturellement à celles d’inversion et de polaires. Ces outils pédagogiques, disparus des programmes scolaires, sont au cœur de la naissance du concept de dualité et des représentations de géométrie non euclidienne.
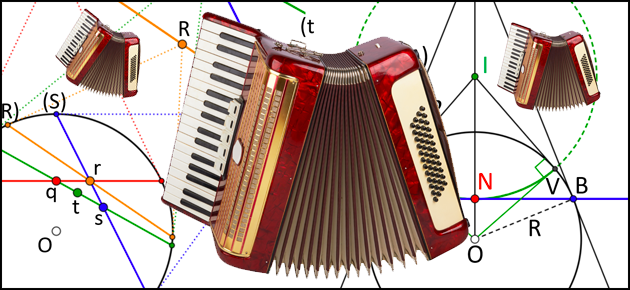
Pour une demi-droite issue d’un point O qui coupe un cercle (C) aux points A et B, le produit  = \overline{\text{OA}} \times \overline{\text{OB}})
définit la puissance du point O par rapport au cercle (C). Cette notion peut être simplement définie avec celle d’angle inscrit et l’ancestral théorème de Thalès. C’est en l’étudiant que Jakob Steiner découvrit, en 1824 seulement, l’inversion, une transformation dont tous les éléments étaient pourtant connus depuis Euclide.
L’inversion, l’autre thème
Une inversion i de pôle O est, comme les symétries, une transformation involutive, donc telle que i composée avec elle-même soit l’identité. Elle fait correspondre à tout point M différent du pôle O le point image, ou homologue, M’ = i(M) sur la droite (OM) tel que 
où k est un nombre réel donné.
En raison de l’analogie manifeste de cette expression avec celle de la puissance d’un point, la constante k est appelée puissance de l’inversion.
Le cercle (C) de centre O et de rayon 
appelé cercle d’inversion, est invariant point par point et est la frontière entre les points intérieurs et extérieurs échangés par l’inversion. Tout point N du segment ...
Lire la suite
