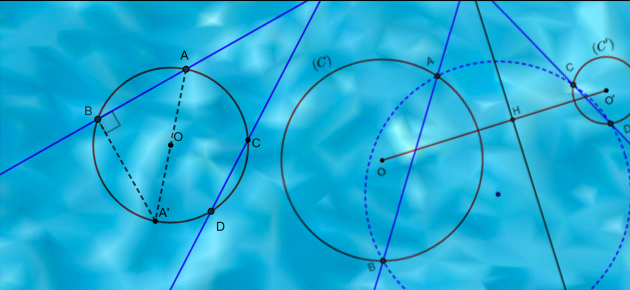
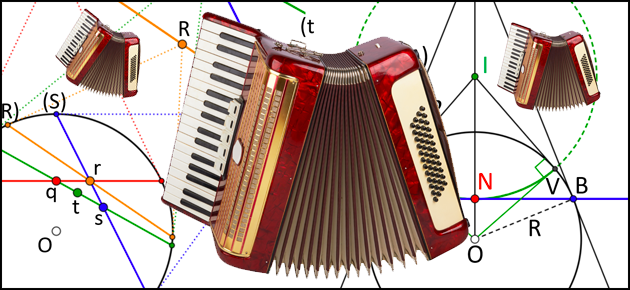
Puissance d'un point
Un point et une courbe : c’est tout ce dont on a besoin pour définir une notion géométrique d’une efficacité redoutable, la puissance d’un point. Le cas le plus connu, bien qu’aujourd’hui absent des programmes scolaires, est la puissance d’un point par rapport à un cercle, ou plus généralement par rapport à une conique.
Dès l’Antiquité, Euclide aurait pu dégager cette notion ! Il faudra pourtant attendre le XIXe siècle pour que Jakob Steiner se lance dans une étude systématique de ces transformations. La puissance d’un point simplifie considérablement les recherches de lieux géométriques et conduit à la notion de dualité, ouvrant ainsi de vastes et nouvelles perspectives.
Dès l’Antiquité, Euclide aurait pu dégager cette notion ! Il faudra pourtant attendre le XIXe siècle pour que Jakob Steiner se lance dans une étude systématique de ces transformations. La puissance d’un point simplifie considérablement les recherches de lieux géométriques et conduit à la notion de dualité, ouvrant ainsi de vastes et nouvelles perspectives.

LES ARTICLES
Une puissance utile
Élisabeth Busser
Parler de « puissance d’un point par rapport à un cercle » peut paraître de nos jours suranné. Pourtant, cette jolie notion géométrique a eu son heure de gloire et son utilité. Ses applications à diverses questions mathématiques sont très fécondes.
Une notion qui vient de loin
François Lavallou
La puissance d’un point par rapport à un cercle apparaît implicitement dès le livre III des Éléments d’Euclide. Cette notion, somme toute élémentaire, sera redéfinie au XIXe siècle et sera à la base de nombreuses applications en géométrie.
L’inversion de la puissance
François Lavallou
La notion de puissance définie par rapport à un cercle amène naturellement à celles d’inversion et de polaires. Ces outils pédagogiques, disparus des programmes scolaires, sont au cœur de la naissance du concept de dualité et des représentations de géométrie non euclidienne.
En bref : Dans les classes des années 1960
Élisabeth Busser et Daniel LignonDans ce programme des années 1960, les transformations géométriques étaient étudiées de manière relativement complète. On y trouvait, bien sûr, les translations (vues en classe de seconde) et le groupe qu’elles formaient.