
Le nombre d’or
Le nombre d’or résulte du partage d’un segment en « moyenne et extrême raison » comme le disait Euclide au IIIe siècle avant notre ère, c’est-à-dire en deux segments, l’un plus grand, de longueur a, l’autre plus petit, de longueur b, tels que . Posons, pour calculer sa valeur,
. Alors, ce nombre x est la solution positive de l’équation x2 = x + 1. On le note φ ; sa valeur exacte est
soit environ 1,618.
Si certaines de ces « tablettes mathématiques » que sont les sangaku sont élémentaires, géométriquement parlant, d’autres font parfois appel à des propriétés beaucoup plus sophistiquées, engendrant des calculs ardus. Même si le célèbre nombre d’or intervient souvent en géométrie (voir notre dossier « La vérité sur le nombre d’or », Tangente 203, 2022), peu de ces « énigmes sur bois » des temples japonais y font appel. Voici les sangaku que nous avons su trouver faisant intervenir le nombre d’or.
Commençons simplement…
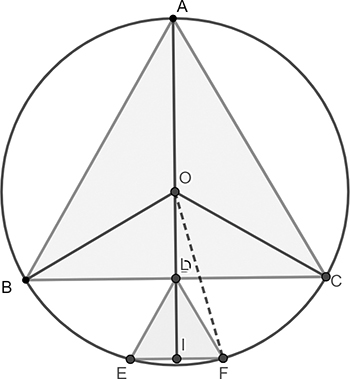
Un premier exemple.
Dans ce premier exemple, les données sont le triangle équilatéral ABC, inscrit dans un cercle dont O est le centre, et, D étant le milieu du côté [BC], le triangle DEF, équilatéral lui aussi, et ... Lire la suite
