
Les sangaku sont une source inépuisable d’émerveillement géométrique. Les figures proposées et les relations métriques qu’elles mettent en évidence revêtent une dimension particulièrement esthétique. Certaines figures sont devenues des classiques de la géométrie. C’est par exemple le cas du dessin proposé sur une tablette datée de 1820 et exposée dans la préfecture de Miyagi (Honshu), sur lequel figurent deux cercles tangents entre eux et à une même droite. Le but du jeu est d’exprimer la distance séparant les points de contact entre la droite et les cercles en fonction des rayons r et R de ses derniers.
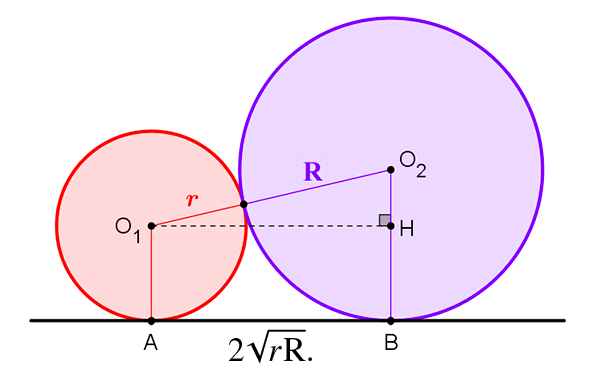
La résolution découle directement de l’application du théorème de Pythagore dans le triangle O1HO2. On a AB2 = O1O22 – O2H, et comme O1O2 = r + R et O2H = R – r, de simples calculs finissent par donner
Le classique des classiques
Une autre figure, liée à la précédente, est emblématique de la période Wasan (XVIIe siècle). Elle est exposée dans la préfecture de Gunma (Honshu), région montagneuse au nord de Tokyo, et est datée de 1824. Reprenez les deux cercles précédents et insérez un petit cercle qui soit tangent aux deux plus grands et ... Lire la suite
