Le dual du rectangle
Voici quelques propriétés du losange :
1. tous les côtés sont de longueur égale ;
2. les angles opposés sont de mesure égale ;
3. les diagonales se coupent selon des angles de mesure égale ;
4. c’est un parallélogramme possédant deux côtés consécutifs de même longueur ;
5. les axes de symétrie partagent en deux les angles opposés ;
6. il possède un cercle inscrit : son centre est à égale distance des côtés.
Comparons avec certaines caractéristiques du rectangle :
1. tous les angles sont de mesure égale ;
2. les côtés opposés sont de longueur égale ;
3. les diagonales sont de longueur égale ;
4. c’est un parallélogramme possédant deux angles consécutifs de même mesure ;
5. les axes de symétrie partagent en deux les côtés opposés ;
6. il possède un cercle circonscrit : son centre est à égale distance des sommets.
Dans les propriétés du losange, remplacez les mots « côté » et « longueur » par « angle » et « mesure », et inversement : vous retrouvez celles du rectangle, mis à part la dernière qui est un peu plus subtile. En raison de cette analogie, on dit que le losange est le dual du rectangle (le carré est son propre dual). Cette dualité que l’on peut définir pour les quadrilatères est valable en géométrie euclidienne.
On ne confondra pas cette dualité avec celle rencontrée en géométrie projective (voir Tangente 189, 2019) entre points et droites, illustrée par : « par deux points distincts, passe une seule droite » et « deux droites distinctes se coupent en un seul point ».
Dans les pavages de Penrose
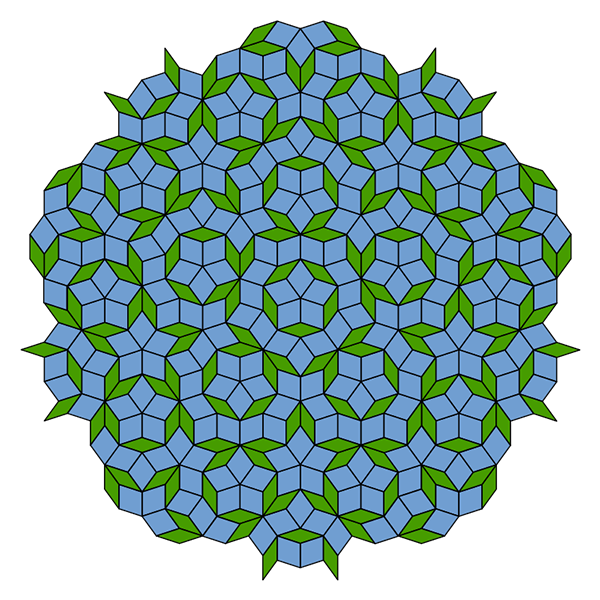
Quand on cherche des pavages avec des losanges, on trouve immédiatement des motifs périodiques (comme tout quadrilatère, un losange quelconque permet de paver le plan). Il existe également des pavages de Penrose (voir Tangente 198, 2021), et notamment le type P3. Il s’agit de pavages construits avec deux losanges particuliers (un « fin » dont le plus petit angle est égal à 36° et un « gros » dont le plus petit angle est cette fois égal à 72°) liés au nombre d’or.
Un pavage de Penrose de type P3.
En fait, il existe une infinité de tels pavages. Ils ont été découverts dans les années 1970 par le mathématicien et physicien britannique Roger Penrose, né en 1931, prix Nobel de physique en 2020 (voir notre dossier dans Tangente 198). Ces pavages sont tous non périodiques, c’est-à-dire qu’il n’existe pas de translation les laissant invariants.
En dehors de leur intérêt artistique, ces pavages servent de modèles aux quasi-cristaux : ce sont des solides qui se comportent comme les cristaux classiques mais dont la structure n’est pas périodique. Cette découverte en 1982 a valu à son auteur, le scientifique israélien Dan Shechtman, né en 1941, le prix Nobel de chimie en 2011.
Hex : des hexagones sur un losange
Le jeu de Hex a été créé en 1942 par le physicien danois Piet Hein (1905‒1996) sous le nom de Polygone. Il a ensuite été réinventé indépendamment en 1948 par le mathématicien américain John Nash (1928‒2015), qui l’a fait connaître dans le milieu scientifique. Le jeu est depuis 2011 édité par le Comité international des jeux mathématiques (CIJM).

Le plateau de Hex.
Les deux joueurs, Blanc et Noir, posent alternativement leurs pions sur un plateau 8 × 8 en forme de losange dont les cellules constituent un réseau à mailles hexagonales : chaque case n’appartenant pas au bord du plateau possède six voisines accessibles par un côté. Il n’y a ni prise, ni déplacement des pions. Le premier joueur à avoir relié les deux bords de sa couleur par une ligne continue formée avec des pions de sa couleur a gagné la partie. L’une des caractéristiques de Hex est qu’il ne peut y avoir de partie nulle.
Retrouvez Hex ainsi que des dizaines d’autres jeux dans Mathématiques et Jeux de société, Bibliothèque Tangente 83, 2023 !