
Les travaux d’Yvonne Choquet-Bruhat se situent dans le champ des mathématiques de la relativité générale. Pour les comprendre ainsi que découvrir qui était cette mathématicienne de très haut vol, première femme à entrer à l’Académie des sciences en 1979, Tangente a contacté l’un de ses anciens collègues, Piotr Chruściel, professeur de physique gravitationnelle à l’université de Vienne.

Piotr Chruściel en 2005.
Tangente : Tout d’abord, quand et comment avez-vous rencontré Yvonne Choquet-Bruhat ?
Piotr Chruściel : Nous nous sommes rencontrés la première fois en 1983, alors que j’étais encore en thèse. J’étais un des participants de l’École de physique des Houches* où Yvonne donnait une série de cours [elle avait alors 60 ans, NDLR]. Il y avait également Stephen Hawking, qui ne pouvait déjà presque plus parler de façon compréhensible : un de ses thésards répétait à voix haute ce que Hawking exprimait (il n’avait pas encore un synthétiseur de voix à l’époque). On s’est ensuite croisés quelques fois. Mais c’est en 2006, lorsque j’avais un doctorant qui travaillait sur les équations d’Einstein, que nous nous sommes côtoyés plus longtemps, à l’institut Max-Planck à Potsdam. Nous y discutions des résultats obtenus par elle, par mon étudiant et par moi-même, ce qui a abouti à notre premier travail commun. Il a néanmoins fallu attendre 2008 pour commencer à véritablement travailler avec elle.
(* Fondée en 1951 par la physicienne Cécile DeWitt-Morette dans la ville des Houches en Haute-Savoie, l’École de physique des Houches propose des cours et des ateliers de haut niveau et accueille des chercheurs du monde entier. De nombreux lauréats du prix Nobel y sont passés.)
Je copilotais, à l’institut Mittag-Leffler dans la banlieue de Stockholm, un programme de recherche intitulé « Géométrie, analyse et relativité générale ». Je l’ai évidemment invitée à y participer, ce qu’elle a accepté malgré un âge déjà avancé (85 ans !). Pour l’anecdote, cet institut était initialement la résidence du mathématicien suédois Gösta
Mittag-Leffler, qu’il a ensuite léguée pour en faire un centre de recherche en mathématiques. C’est une magnifique maison qui surplombe un des nombreux lacs de l’archipel de Stockholm et, comme j’étais l’un des organisateurs, j’avais un très beau bureau ; lorsqu’Yvonne est arrivée, je ne pouvais pas lui donner un bureau moins beau que le mien, donc je le lui ai cédé et suis allé travailler dans un bureau plus petit. Il me semblait inconcevable de ne pas l’accueillir comme il se devait.

Vue de l’institut Mittag-Leffler.
Vous avez travaillé ensemble sur les équations d’Einstein, sujet sur lequel Yvonne Choquet-Bruhat a fait ses premiers travaux.
Albert Einstein a établi des équations, mais le problème est de cerner les solutions de ces équations. Yvonne a réalisé en 1952 (voir encadré) le travail immense et pionnier de montrer comment on peut paramétrer ces solutions et étudier leurs propriétés mathématiques. Il ne s’agit pas de méthodes d’approximation, de troncature ou d’hypothèses simplificatrices, mais bien d’un travail rigoureusement mathématique. Je précise que, dans le domaine de la physique, ce qui a été fait auparavant est très louable, de même ce qui est fait depuis. Mais, à la différence de ce qu’Yvonne a démontré, il ne s’agit pas de méthodes exactes. Elle n’a d’ailleurs pas mis au point une liste de solutions mais plutôt un outil pour les décrire. Cela offre une façon exacte de construire des espaces-temps, et ainsi comprendre la structuration mathématique des équations
d’Einstein, lui qui n’avait pas eu la prétention de faire des maths, mais bien de la physique. En gros, on peut résumer son résultat le plus important, qui est au cœur de la compréhension mathématique des équations d’Einstein, comme ceci : pour toutes données initiales pour les équations d’Einstein, il existe un unique espace-temps qui est maximal (la notion de maximalité en géométrie différentielle signifie à peu près qu’on ne peut pas prolonger plus l’objet) dans la classe d’espaces-temps qui ont de bonnes propriétés causales (ces « bonnes propriétés causales » sont, par exemple, liées au fait que le voyage dans le temps n’est pas permis dans les espaces-temps construits par Yvonne).
Le théorème de 1952
Yvonne Choquet-Bruhat publie en 1952 un article intitulé Théorème d’existence pour certains systèmes d’équations aux dérivées partielles non linéaires. L’article s’intéresse aux équations d’Einstein, qui ne sont pas la célèbre formule E = mc 2. Il présente une équation aux dérivées partielles décrivant comment la matière et l’énergie modifient la géométrie de l’espace-temps, la courbure créée étant interprétée comme un champ gravitationnel. Voici, pour le simple plaisir des yeux, l’équation :
Rμv – 1/2 gμv R + Λgμv = κTμv , avec Rμv le tenseur de Ricci, R la courbure scalaire, gμv le tenseur métrique, Λ la constante cosmologique, Tμv le tenseur énergie-impulsion, κ la constante gravitationnelle d’Einstein égale à 8πG/c4.
Une des questions fondamentales est de savoir si ces équations possèdent une solution unique et bien définie à partir de conditions initiales données. C’est ce qu’on appelle un problème de Cauchy : peut-on prédire l’évolution de l’espace-temps si l’on connaît son état initial ? Yvonne Choquet-Bruhat démontre, dans son article de 1952, un théorème d’existence et d’unicité pour un certain type de systèmes d’équations aux dérivées partielles non linéaires, et, en particulier, pour les équations d’Einstein.
Auparavant, la relativité générale reposait largement sur des solutions particulières. Le théorème confère ainsi une base mathématique et prouve que l’espace-temps peut être décrit de manière rigoureuse par une évolution déterministe à partir de conditions initiales.
Représentation de la Terre affectant la courbure de l’espace-temps.
Dans son livre, Une mathématicienne dans cet étrange univers, elle évoque ses échanges avec Einstein. Vous en a-t-elle parlé ?
Yvonne m’a effectivement raconté qu’elle était très émue lors de sa rencontre avec Einstein, qui s’est montré très gentil avec elle. Néanmoins, l’idée générale qui est sortie de leur entretien autour de son théorème de 1952 peut grosso modo se résumer comme ceci : « c’est très bien mais sans plus. » Cela est dû au fait que cet aspect purement mathématique travaillé par Yvonne n’était absolument pas une préoccupation d’Einstein. Lui faisait des modèles physiques : on prend des équations, puis des solutions exactes dans des cas simplifiés, enfin on extrapole. Elle, au contraire, a fait un travail purement mathématique avec l’idée d’identifier des propriétés de l’ensemble des solutions.
Avec Einstein
« Des souvenirs particulièrement importants pour moi sont les conversations que j’ai eu la chance d’avoir avec Albert Einstein. Après avoir écouté une des conférences de Leray, je sortis de la salle avec lui. Alors que nous parcourions le couloir nous avons rencontré Einstein qui se dirigeait vers son bureau, une grande et confortable pièce qui est devenue un lieu de pèlerinage après sa mort. Les deux hommes se connaissaient déjà, Leray me présenta à Einstein comme une élève de Lichnerowicz qui avait fait sa thèse sur la relativité générale. Il lui dit aussi que j’étais la fille du physicien Georges Bruhat, mort en déportation. C’était pour Einstein une double recommandation, car il sympathisait avec les victimes du nazisme et il estimait le travail de Lichnerowicz qui avait démontré rigoureusement, sous des conditions de stationnarité, une conjecture que lui-même avait faite sur les espaces-temps satisfaisant ses équations et démontré sous des conditions moins générales (staticité) en collaboration avec Pauli. Einstein, l’air bienveillant, me fit donc entrer dans son bureau. J’étais alors une jeune femme et lui un homme déjà âgé, mais d’aspect plaisant avec ses abondants cheveux blancs, bien vêtu quoiqu’en pull et pantalon, et portant des chaussettes dans ses chaussures malgré la légende. Il me demanda aimablement d’exposer ma thèse sur son tableau noir, il me dit de parler français car il comprenait cette langue, mais qu’il me répondrait en anglais car il avait perdu la pratique du français. Je lui exposai mon travail dans ses grandes lignes. Einstein m’écouta avec intérêt, il me félicita et m’invita à frapper à sa porte autant que j’en aurais envie. Il ajouta que la prochaine fois, je devrais parler anglais, car il me fallait m’y habituer. Le libre accès au bureau d’Einstein était une grande faveur, car ce grand homme offrait peu d’occasions de rencontre, il ne venait jamais au thé traditionnel ni aux réceptions. »***
Pourtant, ce théorème est très important.
Fondamental ! J’aime dire qu’Yvonne est la mère des mathématiques de la relativité. Les équations d’Einstein sont une chose plutôt compliquée, que les physiciens ont décortiquée de manière très intéressante mais, en ce qui concerne les mathématiques, son article est vraiment le premier qui ouvre la théorie : il montre qu’on peut construire toutes les solutions des équations d’Einstein à partir de données initiales, ce qui n’était pas connu. Cela dit, force est de reconnaître qu’il a fallu du temps pour qu’on apprécie le théorème : à l’époque, s’intéresser aux mathématiques de la relativité générale était une occupation de niche. En revanche, aujourd’hui, c’est devenu une branche honorable des mathématiques. C’est sans doute grâce à trois grands résultats : le théorème d’Yvonne de 1952, le théorème d’Yvonne et de Robert Geroch de 1970 sur le fait que le domaine de dépendance détermine l’évolution d’un espace-temps, et le théorème de Richard Schoen et Shing-Tung Yau de 1979 sur le fait que la masse d’un espace-temps asymptotiquement plat est positive.
En 2002, vous avez organisé une summer school pour célébrer les 50 ans du théorème.
C’était au mois d’août à Cargèse en Corse. Depuis les années 60, il existe un Institut d’études scientifiques de Cargèse rattaché à l’université de Corse. Il y avait du beau monde qui s’était réuni pour célébrer Yvonne : Robert Geroch, Jean-Pierre Bourguignon, Jim Isenberg, Vincent Moncrief, Robert Bartnik, Sergiu Klainerman… Quand on regarde la liste des élèves de cette École d'été, c’est un plaisir de voir que beaucoup d’entre eux sont devenus des fameux chercheurs dans notre domaine.
Tout en humilité et en humour
« J’ai fait un nouveau séjour au Centre de physique théorique de Cargèse en 2002. Piotr Chrusciel et Helmut Friedrich y avaient organisé une école d’été intitulée The Einstein Equations and the Large Scale Behavior of Gravitational Fields (« Comportement à grande échelle des champs gravitationnels »), sous-titré Fifty Years of the Cauchy Problem. Les conférences données à cette école ont été publiées chez Birkhauser. Dans la préface, les éditeurs, Helmut et Piotr, qualifient ma thèse de 1952 de « travail fondateur » (en anglais breakthrough, pas founding qui signifie « qui procure des fonds », comme avait dit le présentateur à l’amusement des auditeurs), et ils me dédient le livre avec quelques phrases très flatteuses sur mes travaux ultérieurs. À la fin du séjour, une petite fête a été organisée, et Bob Geroch a été chargé de faire un discours. Je ne recherche pas les honneurs, mais les aimables propos de Bob m’ont fait plaisir. »***

Golfe de Cargèse. La photographie du haut, prise par Robert Bartnik,
est la préférée d’Yvonne Choquet-Bruhat.
On reconnaît Piotr Chruściel en 4e position en partant de la gauche.

Yvonne Choquet-Bruhat avec Jim Isenberg, sonnant la cloche pour le déjeuner.
Revenons à votre collaboration avec Yvonne. Pouvez-vous nous parler du théorème que vous avez démontré ensemble ?
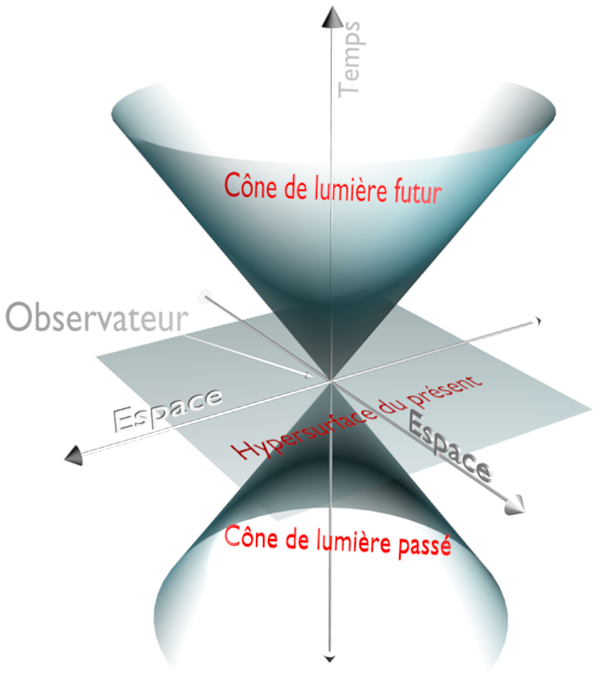
Il s’agissait de notre deuxième article en commun. Nous avons commencé à collaborer au sein de l’institut Mittag-Leffler sur les solutions des équations d’Einstein dans un cône de lumière**. Après avoir « nettoyé » le problème, nous avons démontré un joli théorème qui montre de façon très imagée le fait que la gravité est une force attractive pour l’espace-temps. Plus précisément, le théorème dit ceci : on prend un point et on envoie des rayons lumière dans toutes les directions puis on mesure l’aire que forme le front d’onde à chaque instant. Si on accepte les équations d’Einstein et qu’on est soit dans le vide soit dans un champ de matière à énergie positive, alors la surface est plus petite que celle qu’on a dans l’espace de Minkowski et on a l’égalité si et seulement si on est dans l’espace de Minkowski. Cela montre que les distances d’espace diminuent quand on y met de la matière ou du champ gravitationnel. Je précise que cet article nécessitait, outre des questions mathématiques, une certaine puissance computationnelle pour résoudre des calculs formels très lourds, ce qui nous a été permis grâce à une collaboration avec José Martin Garcia. Cette recherche à l’institut Mittag-Leffler a abouti à plusieurs articles communs, qui se trouvent avoir été quasiment ses derniers articles.
(** L’espace de Minkowski modélise l’espace en trois dimensions ainsi que le temps, quatrième dimension de l’espace. Il a la particularité d’être dépourvu de gravité : il est « plat » car il représente le vide absolu. On appelle cône de Minkowski un cône de lumière dans l’espace de Minkowski. Dans l’espace de Minkowski, la lumière se propage à la vitesse c, donc le front d’onde a un rayon ct, dont l’aire vaut 4πc 2t 2.)
Pouvez-vous enfin nous parler de sa personnalité ?
Elle était très simple, gentille et modeste. Cela peut sembler une banalité mais c’est vrai. C’était un plaisir d’être avec elle et avec nos amis communs. Mon épouse adorait Yvonne. J’aurais aimé continuer à travailler avec elle car elle avait une manière d’aborder les choses très originale, une imagination mathématique fantastique. Vous savez, quand on a un problème mathématique à résoudre, il faut trouver une voie d’approche : on essaie telle ou telle technique, on tente de transformer le problème en un problème équivalent… Tout le monde, dans le métier, connaît beaucoup d’astuces pour arriver à creuser un problème. Mais Yvonne, elle, avait toujours des idées pour contourner les difficultés, elle savait mettre ensemble les bonnes astuces pour aboutir à une résolution. C’est une chose qui demande beaucoup d’inventivité. Du point de vue mathématique, c’était l’une de ses très grandes qualités.
Une mathématicienne aux multiples distinctions
En 1923 naît Yvonne Bruhat, fille de Georges Bruhat, physicien et directeur de l’École normale supérieure. Elle obtient le baccalauréat en 1941, puis intègre l’École normale supérieure de jeunes filles à Sèvres. En 1946, elle est reçue première à l’agrégation de mathématiques. Dès lors, professeur assistante à l’École normale supérieure puis assistante de recherche au CNRS, elle soutient, en 1951, sa thèse (préparée sous la direction d’André Lichnerowicz) contenant son fameux théorème. Elle passe ensuite un an à l’Institute for Advanced Study de Princeton puis devient maîtresse de conférences à l’université de Marseille, puis à Reims et enfin à Paris où elle devient professeur de mécanique analytique et de mécanique céleste.
Les distinctions ne manquent pas, même si elle n’a jamais couru après les honneurs : médaille d’argent du CNRS en 1958, prix Henri-de-Parville de l’Académie des sciences en 1963, première femme élue à l’Académie des sciences dans la section mécanique en 1979, présidente du Comité international de relativité générale et gravitation entre 1980 et 1983, élue à l’Académie américaine des arts et des sciences en 1985, prix Noether Lecture de l’Association for Women in Mathematics en 1986 et 2006, prix Dannie-Heineman de physique mathématique de la Société américaine de physique et de l’American Institute of Physics en 2003 ainsi que le très prestigieux prix Marcel Grossmann Award en 2004.
Côté vie personnelle, elle se marie en 1947 avec le mathématicien Léonce Fourès (elle signe ses premiers articles sous le nom Yvonne Fourès-Bruhat) puis épouse en 1961 Gustave Choquet, mathématicien éminent et académicien des sciences. Elle a avec lui deux enfants, dont Daniel Choquet, neurobiologiste, lui aussi académicien des sciences.

Yvonne Choquet-Bruhat en 1974.
Une petite fille devenue l’une des plus grandes savantes du siècle
« J’ai eu la chance d’avoir des parents intelligents et cultivés, une littéraire et un scientifique qui aimaient leurs enfants et souhaitaient les faire bénéficier de leurs connaissances théoriques et pratiques. Dès que ma raison s’est éveillée, j’ai désiré comprendre quelque chose de cet univers étrange où nous vivons, et de ce qu’y font les êtres humains, moi en particulier. Je me vois encore dans la chambre de mes parents leur posant une question sur l’étrangeté qu’était pour moi le fait que je n’avais une directe conscience que de moi-même. Ma mère dit à mon père « elle cultive le solipsisme » et mon père répondit « la métaphysique ça rend fou ». La question et les réponses sont toujours d’actualité. Je n’ai cependant pas cultivé le solipsisme, un mot savant qui ne résout rien. J’ai toujours cru qu’il existait en dehors de moi-même une réalité qu’à peine sortie de l’enfance j’ai désiré comprendre. […] Dans mon adolescence j’ai flirté avec des domaines variés de la connaissance : sciences naturelles, physique, histoire, philosophie. Cette dernière englobait autrefois toutes les sciences, cette généralité a été rendue impossible par le gigantesque accroissement de chacune d’entre elles. Je suis finalement devenue une mathématicienne travaillant sur des problèmes posés par la physique. »***
(*** Les citations sont extraites de l’ouvrage d’Yvonne Choquet-Bruhat Une mathématicienne dans cet étrange univers (Odile Jacob, 2016).)
