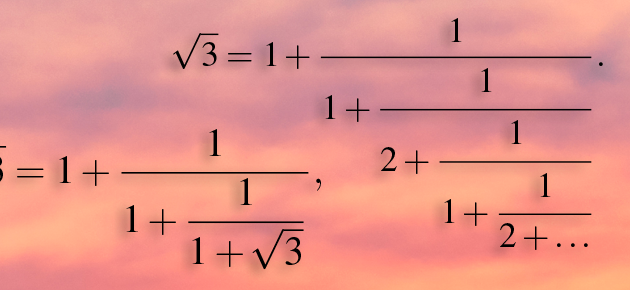
Dans l’histoire des mathématiques, la notation décimale est relativement récente : sans doute introduite par les mathématiciens arabes, elle est vulgarisée de manière indépendante par le Flamand Simon Stevin (1548‒1620). Elle est très vite devenue incontournable. À l’heure actuelle, avec l’utilisation des calculateurs numériques, que ferait-on sans cette écriture ?
Avant la notation décimale
Auparavant, l’écriture fractionnaire était utilisée. Ainsi, chez les Égyptiens, le nombre 2,75 s’écrivait (avec les notations actuelles) 2 + 1/2 + 1/4. Ce type d’écriture perdura jusqu’au XVIe siècle. Mais comment faire pour représenter des nombres irrationnels, qui, par définition, ne possèdent pas d’écriture fractionnaire ? C’est là qu’interviennent les fractions continues !
La notation en fraction continue est liée à l’algorithme d’Euclide.
Il s’agit de représenter un nombre x sous la forme
avec α, β, γ… entiers, c’est-à-dire en utilisant uniquement des fractions dont le numérateur vaut 1.
Par exemple, on peut écrire 47/6 de la manière suivante :
Ainsi, quand le reste de la division euclidienne vaut 1, l’algorithme s’arrête. Cela se produit pour toutes les fractions. Par contre, lorsque qu’un nombre n’est pas rationnel, son développement en fraction continue est infini.
Cherchons par exemple le développement en fraction continue de
d’où :
On abrège cette dernière écriture, qui se répète indéfiniment, la barre indiquant que le chiffre 2 se répète à l’infini.
Pour autant, il n’est pas toujours aisé de trouver le développement en fraction continue d’un radical ! Amusez-vous à trouver celui de par exemple (voir un algorithme de calcul ainsi que le résultat en encadré).
D’une écriture à l’autre
Le procédé de développement d’une racine en fraction continue est explicité ci-dessous pour l’exemple de Il s’agit d’un enchaînement des trois mêmes opérations : exprimer la partie entière ; inverser une fraction pour obtenir un numérateur unitaire ; utiliser une forme conjuguée pour supprimer la racine du numérateur.
La partie entière de vaut 1, donc
(avec X une expression que l’on cherche à déterminer).
Or,
En utilisant la forme conjuguée, on obtient :
Or,
On en déduit
c’est-à-dire
On peut donc écrire
À l’inverse, quel nombre se cache derrière le plus simple des développements en fraction continue périodique, à savoir
soit encore
En notant X cet inconnu, on peut écrire
Notre nombre X, visiblement positif (et même strictement supérieur à 1), est donc solution de l’équation X2 ‒ X ‒ 1 = 0.
Donc
On retrouve le nombre d’or, bien connu de nos lecteurs !
Références
• Dossier « La vérité sur le nombre d’or ». Tangente 203, 2022.
• Itération et récurrence. Bibliothèque Tangente 76, 2021.
• Les algorithmes. Bibliothèque Tangente 37, 2013.
Les lecteurs pourront s’exercer à retrouver
ou encore
cette dernière égalité a été établie pour la première fois par Raffaele Bombelli (1526‒1572), qui publie sa méthode de calcul dans L’Algebra l’année de sa mort.
Utile pour les approximations !
Les développements de toutes ces racines sont périodiques. C’est en fait le cas pour tous les nombres quadratiques, c’est-à-dire qui sont solution d’une équation du second degré à coefficients rationnels. Ce résultat a été montré par Lagrange en 1770. La réciproque avait été démontrée auparavant par Euler en 1748.
Pour les nombres non quadratiques, le développement est infini et non périodique.
Au XIXe siècle, les fractions continues furent l’objet d’un nombre inouï de travaux. Elles étaient connues, utilisées et enseignées par tous les mathématiciens, dans tous les pays. Dans n’importe quel livre d’enseignement de cette époque, on trouve un chapitre sur le sujet.
Mais quel est l’intérêt de ces développements ?
Reprenons l’écriture
Notons α 0 = 1 ; α 1 = [1, 2] ; α 2 = [1, 2, 2] ; α 3 = [1, 2, 2, 2] ; et ainsi de suite.
En effectuant les calculs (il suffit de tout réécrire sous forme fractionnaire et de mettre les quotients obtenus sous forme irréductible), on obtient :
α 0 = 1 ;
α 1 = 3/2 = 1,5 ;
α 2 = 7/5 = 1,4 ;
α 3 = 17/12= 1,4166… ;
α 4 = 41/29 = 1,4136…
Les lecteurs, qui savent tous que , peuvent constater que la suite des αi semble converger vers
en prenant alternativement des valeurs supérieures et inférieures. Ce comportement se retrouve pour le développement de tous les types de nombres, aussi bien rationnels que non quadratiques, ce qui peut s’avérer bien pratique si l’on vit dans un siècle où les calculatrices n’existent pas et que l’on veut obtenir rapidement de « bonnes » approximations…
Une généralisation
L’article traite du cas très particulier de fractions continues : elles sont ici unitaires (tous les numérateurs sont égaux à 1) et n’utilisent que des signes +. En dépassant ces contraintes, on trouve d’autres manières de représenter des racines.
Par exemple, en utilisant l’écriture A = a2 + r d’un nombre A comme somme d’un carré a2 et d’un résidu r,
on obtient
soit encore
une égalité dont on tire :


