Le premier souci lorsqu’un enfant (ou un adulte) apprend à faire du vélo est celui de l’équilibre et de la stabilité. Des études ont montré que pour obtenir une bonne stabilité, il faut que l’axe de la fourche avant vienne en avant du point de contact de la roue avant avec le sol.
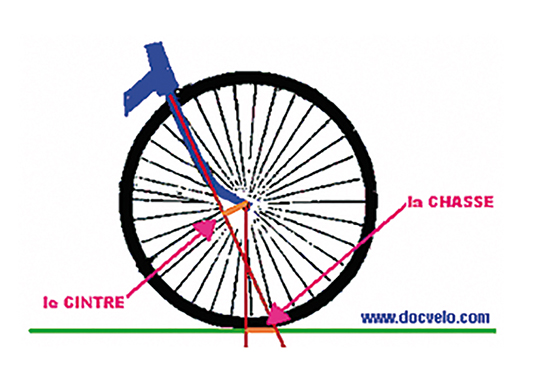
Plus l’écart entre les deux points (la chasse) est grand, meilleure est la stabilité. Mais les coureurs cyclistes professionnels préfèrent une chasse moins importante, qui donne un vélo certes moins stable mais plus maniable et plus « nerveux ». Un vélo à chasse négative serait, quant à lui, totalement instable.
Penchons nous ensuite sur la notion de braquet. Le braquet est le rapport entre le nombre de dents de la roue dentée du pédalier (le plateau) et celui de la roue dentée du moyeu arrière (le pignon). Plus le braquet est grand, plus on roule vite (à cadence de pédalage égale), mais plus l’effort musculaire est important. En côte, on doit donc réduire le braquet (et la vitesse) afin que l’effort musculaire soit acceptable.
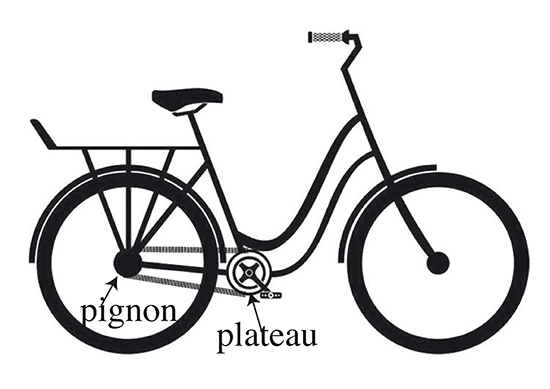
À la notion de braquet b est associé le développement L, qui est la distance parcourue pour un tour complet de pédalier. On a ainsi la formule L = b × π × d, où d est le diamètre de la roue.
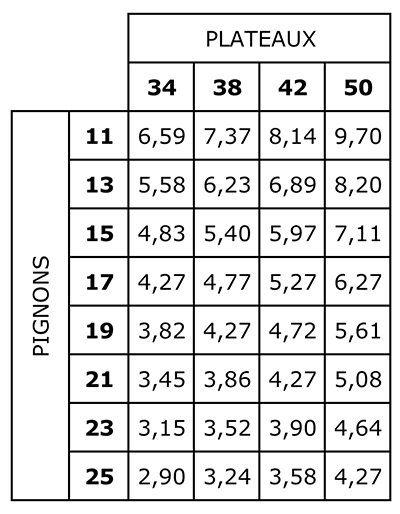
Dans ce tableau, on trouve des développements en mètres correspondant à différents braquets pour une roue d’environ 68 cm de diamètre. Ces développements sont bien sûr approchés. On remarque que les braquets 50 / 25, 42 / 21 et 38 / 19 donnent évidemment le même développement.
Les boyaux de Chris Froome
Voici un extrait du journal La Montagne (daté du 16 juillet 2017) :
« Lors de l’étape de dimanche dernier entre Nantua (Ain) et Chambéry (Savoie), le Maillot jaune Chris Froome avait ainsi opté pour un 36 / 32, pour avaler le mont du Chat (8 km à 10 % de moyenne !). Et il n’était pas le seul. Objectif affiché : privilégier ainsi une fréquence de pédalage plus importante à la force, avec un gain finalement en puissance et une sollicitation moins importante des muscles. »
1. Quel était le développement de ce coureur dans cette côte ? On suppose que sa roue avait un diamètre de 70 cm, soit 73 cm avec le boyau.
Voici maintenant une énigme surprenante que posa Martin Gardner (voir Tangente 136) dans sa rubrique de jeux mathématiques du Scientific American. On tient une bicyclette en équilibre et, à l’aide d’une ficelle, on tire l’une des pédales (positionnée en bas) vers l’arrière.
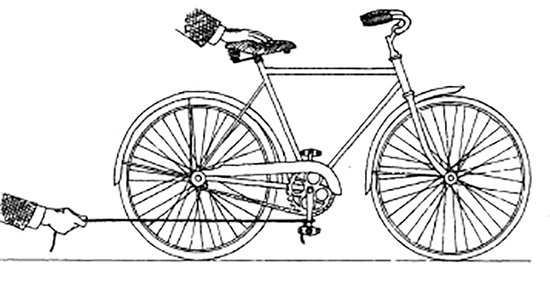
2. La bicyclette se déplacera-t-elle vers l’avant, vers l’arrière, ou restera-t-elle immobile ?

