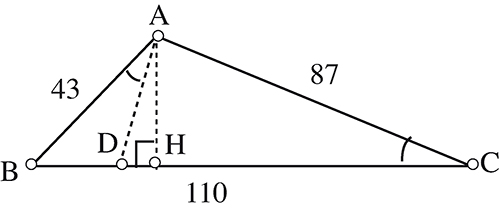
On considère un triangle ABC quelconque. H est le pied de la hauteur issue de A et D est le point de [BC] tel que .
Les triangles ABC et ABD sont semblables et le rapport de leurs aires est égal au carré du rapport de similitude :
Aire (ABD) / Aire (ABC) = (AD / AC)2 = (AB / BC)2 = (43 / 110)2, soit environ 0,153, et BD = BA × 43 / 110 est « proche » de 16,8.
Par ailleurs, Aire (ABC) = BC × AH / 2 et Aire (ABD) = BD × AH / 2, d’où
Aire (ABD) / Aire (ABC) = BD / BC. On en déduit que AD2 / AC2 = BD / BC, d’où AD2 × BC = BD × AC2.
Mais nous avons aussi AC2 = AB2 + BC2 – 2 AB × BC × cos
et AD2 = AB2 + BD2 – 2 AB × BD × cos .
En reportant dans l’égalité précédente, on obtient :
(AB2 + BD2 – 2 AB × BD × cos ) × BC
= (AB2 + BC2 – 2 AB × BC × cos ) × BD.
En divisant les deux membres par BC × BD, on aboutit à :
(AB2 / BD) + BD – 2 AB × cos = (AB2 / BC) + BC – 2 AB × cos
),
d’où (AB2 / BD) – BC = (AB2 / BC) – BD.
En réduisant au même dénominateur dans chaque membre, on trouve :
(AB2 – BC × BD) / BD = (AB2 – BC × BD) / BC.
Enfin, en simplifiant par (AB2 – BC × BD),
on arrive à 1 / BC = 1 / BD, d’où BD = BC.
Où est l’erreur ?

