Les tableaux de fils tendus

Les tableaux de fils tendus ont été une activité manuelle, parfois artistique, qui eut son heure de vogue au siècle dernier. Tantôt figuratifs, tantôt abstraits, ils laissaient souvent apparaître en filigrane des courbes mathématiques.
L’activité consiste à matérialiser des segments de droites par des fils tendus entre des clous fixés sur un support plan. Si cette pratique est tombée en désuétude, elle réapparaît virtuellement avec les logiciels de géométrie dynamique, qui permettent de réaliser numériquement les mêmes dessins (sans les risques de blessures liés à la manipulation du marteau et des clous…).

Une des constructions les plus simples est celle représentée ci-dessous. La méthode de construction apparaît clairement : dans chaque quadrant, on relie le premier clou d’un côté au premier clou du côté perpendiculaire. On continue ensuite en reliant entre eux les clous numéros 2, numéros 3… jusqu’aux clous numéros 8.

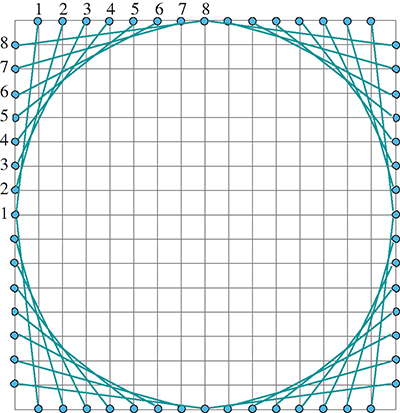
L’ensemble des segments matérialisés par les fils semble « enserrer » une courbe qui ressemble à un cercle (certains sites Internet de string art mal documentés les décrivent d’ailleurs comme des arcs de cercle). Or cette courbe, enveloppe d’une famille de droites, n’est pas un cercle mais la réunion de quatre arcs de parabole. Cette construction pourrait d’ailleurs aussi bien se faire par pliages sur une feuille de papier.
Si la parabole est une courbe que l’on peut faire apparaître de manière élémentaire avec la technique des fils tendus, il est possible de construire d’autres objets mathématiques. Pour rester dans les coniques, comment construire une hyperbole ?
Une méthode consiste à planter des clous régulièrement espacés sur deux cercles extérieurs l’un à l‘autre, puis à relier un point A d’un cercle à un point B de l’autre (B n’étant pas le point symétrique de A par rapport au centre de symétrie des deux cercles). On relie ensuite les points un à un en tournant dans le même sens sur les deux cercles.

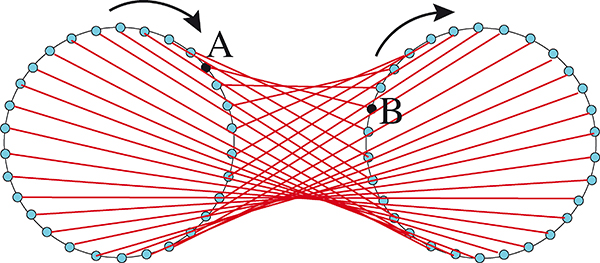
Et l’ellipse ? La construire à l’aide de fils tendus nécessite l’utilisation d’un accessoire, une équerre.

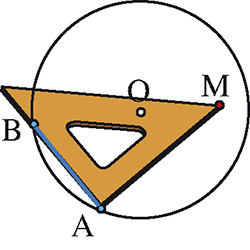
On trace un cercle de centre O et on choisit un point M intérieur au cercle (M étant différent de O sinon l’ellipse serait confondue avec le cercle tracé). On place le sommet de l’angle droit sur le cercle de sorte qu’un des côtés de l’angle droit (ou son prolongement) passe par M. On tend un fil entre les points A et B du cercle situés sur l’autre côté de l’angle droit de l’équerre (ou son prolongement). On répète cette opération en déplaçant le sommet de l’angle droit de l’équerre sur le cercle.

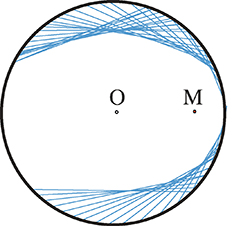
Une ellipse en cours
de construction.