Les briques de Mark Ov sont des parallélépipèdes rectangles ne possédant aucune face carrée. Les dimensions de chaque brique sont entières, dans une certaine unité. De plus, ces briques présentent la particularité que la somme des carrés de leurs trois dimensions est égale au triple de leur produit, à l’instar du cube de côté unité. Un exemple d’une telle brique est le parallélépipède (2, 5, 29), puisque 22 + 52 + 292 = 3 × (2 × 5 × 29) = 870.
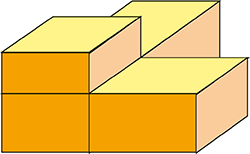
La figure ci-contre, qui ne respecte pas les proportions, montre quatre briques de Mark Ov assemblées en coin. Pour chacune des trois surfaces de contact, les deux dimensions de chacune des deux briques correspondent exactement.
Si les quatre briques sont toutes différentes les unes des autres, quel est le volume minimum de la plus volumineuse d’entre elles ?

