Des couleurs et des bidons

Vous mélangez des peintures à partir des trois couleurs suivantes : rouge, bleu et vert. Quelle teinte allez-vous obtenir ? Pour le savoir, il faut bien sûr connaître les proportions du mélange. Un modèle pratique pour modéliser cette situation est le cube RGB (red, green, blue) conçu pour l’affichage des couleurs sur un écran.

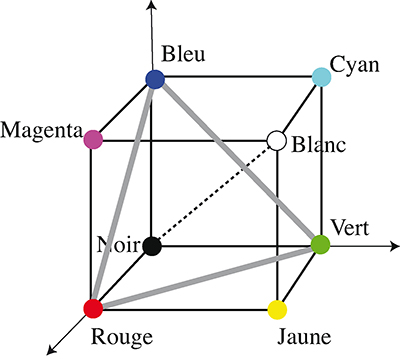
Le cube des couleurs.

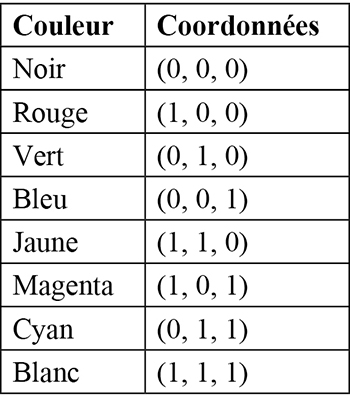
Les trois axes de coordonnées correspondent aux trois couleurs primaires rouge, vert et bleu. Mais pour définir une couleur, il faut tenir compte de deux paramètres : la teinte et la luminosité. Dans le cube, la luminosité se gradue sur un axe reliant les points (0, 0, 0) et (1, 1, 1), du noir au blanc.

Si on ne s’intéresse qu’à la teinte, en faisant abstraction de la luminosité, on se place dans le plan du triangle Rouge-Vert-Bleu dans lequel les trois coordonnées ont une somme constante égale à 1 (ou 100 %). On peut alors représenter le mélange dans un triangle.

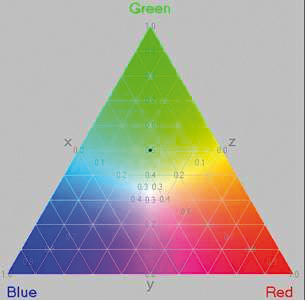
Ce triangle des couleurs a été imaginé par le physicien et mathématicien écossais James Clerk Maxwell (1831-1879). Tout point intérieur au triangle correspond à un mélange des trois couleurs, les trois coordonnées indiquant les proportions respectives des couleurs, dont la somme est égale à 1.

Des questions de transvasement

Le type de problème qui suit apparaît en 1240 dans un texte des Annales de la ville allemande de Stade, près de Hambourg. Il serait dû à l’abbé Albert Abbot.

On dispose de trois récipients non gradués de capacités respectives huit litres, cinq litres et trois litres. Le récipient de huit litres étant plein (d’huile ou de vin), on demande de partager ces huit litres en deux fois quatre litres. La seule opération permise est le versement d’un récipient A dans un récipient B jusqu’à ce que le récipient B soit plein ou que le récipient A soit vide.

On trouve ce problème, ou des variantes, dans de nombreux ouvrages de récréations mathématiques, notamment dans les Problèmes plaisants et délectables de Bachet de Méziriac (1581-1638). La solution est généralement donnée sans explication, le tâtonnement inspiré semblant être la seule méthode utilisée.

Ce n’est qu’en 1939 qu’un physicien et statisticien écossais, Maurice Charles Kenneth Tweedie (1919-1996), publie une méthode de résolution de ce type de problèmes à l’aide des coordonnées trilinéaires.

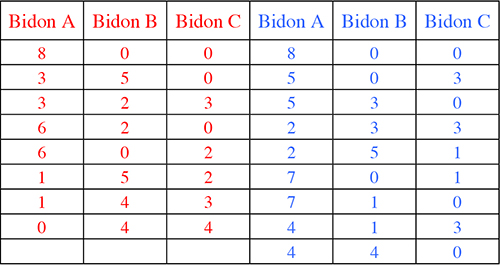
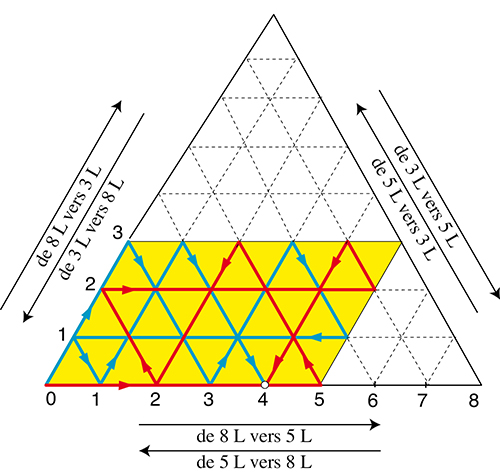
Dans ce diagramme, le point 0 en bas à gauche correspond à la situation (8, 0, 0) où le bidon de huit litres (A) est plein et les deux autres vides. La partie jaune indique la zone dans laquelle la somme des contenus des trois récipients est égale à huit litres, les bidons de cinq litres (B) et trois litres (C) ne pouvant contenir plus que leur capacité. Les tracés rouge et bleu donnent les deux solutions du problème, l’une se faisant en commençant par remplir B et l’autre en commençant par remplir C, la suite se faisant de manière automatique. Le tracé rouge conduit à sept transvasements alors que le tracé bleu en nécessite huit.

À vous de résoudre le même problème dans lequel seul le premier récipient est plein au départ et où il s’agit de partager son contenu en deux parts égales : avec des récipients de 12 l, 7 l et 5 l ; avec des récipients de 16 l, 12 l et 7 l.