
Cet article a initialement été publié dans Tangente 162. Nous le republions à l'occasion du décès de Maryam Mirzakhani.
« Les mathématiciens s'étant rassemblés du monde entier ont remis cette récompense en raison de remarquables écrits?» à Maryam Mirzakhani, mathématicienne iranienne de 37 ans, professeure à la prestigieuse université de Stanford (Californie).
S'adressant à George Sand, Flaubert indiquait : «?L'homme n'est rien, l'œuvre tout ! » Alors parlons de l'œuvre de Maryam Mirzakhani, ou plutôt, aiguisons l'appétit du lecteur, tant les notions mathématiques en jeu sont riches et complexes, tant l'œuvre est conséquente. Quelques références de difficulté graduelle, citées à la fin de l'article, permettront de nourrir les curiosités.
Très brièvement, on peut dire que Maryam Mirzakhani s'est intéressée à certains systèmes dynamiques sur des objets géométriques, dans deux cas principaux.
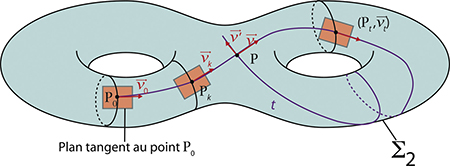
Dans le premier cas (celui d'une surface hyperbolique), le système dynamique étudié est le flot géodésique sur la surface : étant donné un point de départ et une direction, il existe une unique manière d'évoluer, en suivant la ligne de plus court chemin (la géodésique) déterminée (localement, et en fait globalement) par ce point et cette direction.
La question consiste à savoir comment se comportent les trajectoires dans les temps futurs : existe-t-il des trajectoires qui se referment (dites périodiques), voire se referment sans se croiser (périodiques simples) ? Quels renseignements la donnée de ces géodésiques périodiques fournit-elle sur la géométrie de la surface ? etc.
Le second cas (celui des surfaces de translation), s'intéresse au flot vertical sur la surface. Nous nous contenterons ici d'une approche très superficielle de ce cas.
Les scènes de théâtre de la dynamique. L'avant-scène topologique
Le « théorème de classification des surfaces » fait partie du bréviaire de tout apprenti mathématicien : à « déformation continue » près (sans déchirure), une surface « bornée, orientable, sans bord?» se ramène à l'un des objets mathématiques présentés dans l'encadré Le bestiaire des surfaces orientables, caractérisée par son genre g.
Si l'on retire n disques distincts à une surface de genre g, le résultat est une surface de genre g avec n composantes de bord ou n bouts selon que les disques sont ouverts ou fermés, et on notera sans précision Σg,n une telle surface (on la note Σg lorsque n = 0).
On peut construire Σg,n par repliement (identification deux à deux des côtés d'un polygone) et si le polygone a une structure métrique (si on sait mesurer les distances entre points, les angles entre vecteurs, etc.) la surface repliée hérite de cette structure métrique, d'abord localement (entre points voisins) puis globalement.
Scènes géométriques
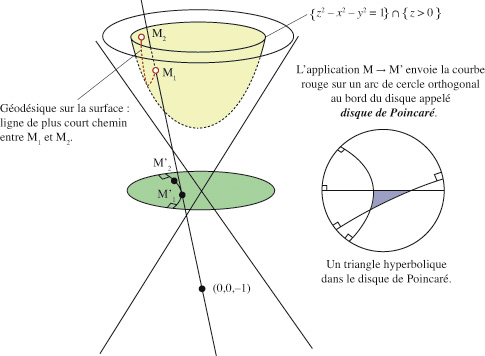
La partie supérieure (située dans le demi-espace {z > 0}) de l'hyperboloïde de révolution à deux nappes d'équation z2 – x2 – y2 = 1 est une surface dont chaque plan tangent peut être muni d'un produit scalaire, objet bien adapté aux calculs métriques (intrinsèques).
On construit naturellement sur cette surface une métrique (dite hyperbolique) qui permet de mesurer les distances entre points et angles entre vecteurs de chaque plan tangent en un point. Pour cette métrique, il existe toujours une unique ligne de plus court chemin joignant deux points, intersection d'un plan passant par O avec la surface. La projection de la surface à partir du point (0, 0, –1) donne un disque ouvert de rayon 1. Si l'on transporte la structure métrique sur le disque (dit de Poincaré), les géodésiques deviennent des arcs de cercle, ou des diamètres, tous orthogonaux au bord.
La métrique du deuxième schéma est une métrique euclidienne (à singularités). Si on se donne n vecteurs du plan euclidien 2 assemblés bout à bout de deux manières, de sorte que les deux lignes polygonales formées ne se croisent pas sauf aux extrémités, on forme un polygone plan. En décrétant d'une part que les deux copies du vecteur
sont identifiées l'une à l'autre et d'autre part qu'une direction de référence (la direction verticale) fait partie de la structure géométrique, on construit, par repliement et de manière formelle, un couple, constitué d'une surface sans bord et d'une direction privilégiée. « De manière formelle?» parce que le genre de la surface peut être observé par le repliement effectif, mais on décide que sur cette surface, les lignes géodésiques sont des segments de droite.
Les surfaces ainsi construites sont dites de translation parce que les applications qui définissent le recollement ne sont que des translations. Cette fois-ci, le repliement ne se passe pas bien : il se forme autour des sommets que l'on identifie entre eux des singularités ; au plan géométrique, on peut dire que la courbure négative se concentre en les points projetés des sommets où se forment les singularités.
Mirzakhani dans le cadre hyperbolique
Sur Σg,n il y a une infinité de manières de mettre une métrique hyperbolique. L'ensemble de ces métriques est classifié par l'espace des modules, Mg,n, qui ne distingue pas deux métriques qui au fond sont les mêmes (on dit isométriques). Fixons pour l'instant une métrique sur Σg,n.
Dessinons sur cette surface un chemin continu qui se referme (un lacet). Si on laisse glisser ce chemin sur la surface, on peut le rendre géodésique d'une seule manière : les mathématiciens disent qu'il existe une unique géodésique périodique dans la classe (d'homotopie libre dans le jargon) du lacet. Il n'existe alors qu'un nombre fini N (L) de géodésiques périodiques de longueur inférieure ou égale à L.
La fonction qui à L associe N (L) contient énormément d'informations sur la géométrie de la surface mais ne peut pas être explicitée. Toutefois, dans les années 1940, l'analyse de Fourier a permis de donner une idée exacte de son comportement asymptotique : L × N(L)e-L → 1 lorsque L tend vers l'infini ; en particulier, la croissance (exponentielle) de ce nombre ne dépend pas du genre de la surface. Dans les années 1980, Joan Birman et Caroline Series ont remarqué que le nombre de géodésiques périodiques simples Ns(L) a une croissance au plus polynomiale en la longueur L. En 2000, Igor Rivin a donné un encadrement de cette fonction de comptage (mais avec des polynômes en L de degrés différents). C'est dans ce contexte que sont venus s'inscrire les premiers résultats de Maryam Mirzakhani. Elle a obtenu dans la première partie de sa thèse le résultat suivant : il existe une constante C, qui dépend de Σg,n, telle que
Ce premier résultat est spectaculaire à double titre?:
• parce qu'il précise de manière optimale le comportement asymptotique de Ns – c'est en soi une avancée majeure !
• parce que les méthodes employées sont nouvelles et que, en définitive, la formule mise en avant n'est qu'une simple conséquence de résultats bien plus profonds, qui procurent une meilleure compréhension de la géométrie (compliquée) de l'espace des modules Mg,n. Par exemple, des méthodes employées résulte une formule de récurrence qui permet de calculer les volumes de tous ces espaces de modules. Une autre illustration de la pertinence de l'approche est qu'elle a redonné – de manière surprenante – une démonstration de la conjecture de Witten (qui porte sur la géométrie des espaces de modules mais dont l'énoncé ne peut pas être donné ici). Au fond, l'approche de Mirzakhani s'affranchit du défaut d'homogénéité de la géométrie de Mg,n. Cette succession de premiers résultats a constitué le contenu de sa thèse. Beaucoup de mathématiciens seraient fiers de les avoir établis au cours de leur carrière.
Dans le cadre des surfaces de translation, les travaux de Mirzakhani portent encore sur l'espace des modules associé, mais ne peuvent être décrits ici.
Laissons la conclusion à Curtis McMullen, directeur de thèse de Mirzakhani, lui-même lauréat de la médaille Fields en 1998 (pour ses travaux en dynamique complexe) : « Les champs d'investigation de Maryam Mirzakhani s'étendent, avec une forte originalité, sur un grand nombre de disciplines des mathématiques – parmi lesquelles la géométrie algébrique et symplectique, la topologie en basses dimensions, les processus aléatoires. Ses avancées ont changé notre vision des espaces de modules et montrent le chemin vers les frontières de la connaissance mathématique, où des questions majeures attendent d'être résolues.?»
