
Étranges objets mathématiques – Mickaël Launay
(Amphithéâtre, 11h45)
Ce n'est pas parce qu'on a des machines que l'on doit se dispenser de réfléchir. Parfois même, leurs défauts nous obligent à redoubler d'ingéniosité. Prenez la calculatrice Caroline commercialisée au milieu du XXe siècle. Chaque roue est associée à un chiffre (unités, dizaines...) et il suffit de les faire tourner d'autant de crans que souhaité pour additionner les nombres voulus. Seulement voilà : les roues ne tournent que dans un sens. Impossible de revenir en arrière et donc de faire des soustractions. Du moins, au premier abord, car remarquez que si vous entrez l'opération 9 999 999 + 1, la machine qui n'a qu'une capacité de sept chiffres vous affichera... 0. On en déduit donc que 9 999 999 = -1. Bref, nous sommes en train de calculer modulo 10 000 000 et de la même façon nous avons -2 = 9 999 998 ou -42 = 9 999 958. Nous voilà à nouveau capables de faire des soustractions ! Si aujourd'hui nos ordinateurs n'ont plus de problèmes pour soustraire, ils ont, comme la Caroline, leurs limites et il incombe toujours aux humains de s'en servir avec astuce et créativité.
Le choix des sons et des rapports de sons en musique – Daniel Justens
(Amphithéâtre, 13h)
La musique est un langage universel. C'est en quoi elle a de nombreux points communs avec les mathématiques. Mais il y a plus : la musique est conceptuellement mathématique. Quand on fait vibrer une corde, celle-ci produit un son. Coupons la corde en deux parties égales et faisons vibrer une des demi cordes. Le son produit ressemble au précédent mais nous le qualifions de « plus aigu ». Musicalement, on associe le même nom, la même note (l'une étant à l'octave de l'autre) aux deux sons que notre cerveau perçoit comme semblables. En fait, la demi corde vibre plus vite que la corde entière, deux fois plus vite. Coupons à présent la corde initiale en trois. Cette fois le son émis par le tiers de corde nous semble différent du son de départ mais la combinaison, l'accord des deux sons nous paraît harmonieux. Le tiers de corde vibre trois fois plus vite. Voilà donc mis en place un système de construction de sons deux à deux agréables à l'oreille. Rien ne nous empêche de poursuivre la procédure. Mais quand faut-il s'arrêter ? On arrête la construction lorsqu'on retombe approximativement sur une des octaves du son de départ. Voilà pourquoi toutes les musiques du monde tablent sur 5, 12 ou 43 sons, dont les puissances de trois sont proches d'une puissance de deux !
D'où vient le vocabulaire mathématique ? – Bertrand Hauchecorne
(Amphithéâtre, 14h45)
Les Grecs ne sont pas les premiers à avoir utilisé les maths mais furent certainement des pionniers pour se poser la question de la démonstration. Ils furent donc des créateurs de mots, ceux nécessaires à développer leurs raisonnements. Dans leur langue, mathemata était le pluriel d'un vocable signifiant aussi bien le fait d'apprendre que son résultat, soit la connaissance puis la science, principalement celle basée sur le raisonnement. Les besoins d'arpentage ont amené à se poser des questions sur les figures les plus simples, cercle, rectangle, etc. : le domaine de la géométrie prenait une place très importante à l'époque. Dans l'Antiquité grecque, la déesse Gê personnifiait la Terre ; ainsi la géométrie était la mesure de la terre. Qui dit démonstration, dit énoncé. Contempler un théorème, c'est observer un spectacle : c'est ce que nous murmure l'étymologie de ce mot ; la racine thea signifiant spectacle se retrouve dans théâtre et dans théorie. Les Grecs ont forgé le concept de nombre, indépendant des objets qu'il compte ; ils le nommèrent arithmos. Ainsi naquit l'arithmétique, la science du nombre. Ces mots vieux de vingt-cinq siècles nous donnent ainsi une vision très poétique des mathématiques et nous rappellent le lien que les anciens avaient avec la Reine des sciences.
Le Chicago, un jeu oulipien – Olivier Salon et Hervé Le Tellier
(Amphithéâtre, 15h45)
Le Chicago est une invention de Paul Fournel permettant de faire deviner un mot, à la façon d'une charade, mais en remplaçant les définitions de la charade par 4 mots du même univers sémantique, aboutissant logiquement à la syllabe à deviner. Par exemple, les prémisses :
• Pont → Y m'rend service
• Voûte → Y m'est utile
• Arcade → Y m'sert
• Portique → Y m'dépanne
conduisent légitimement à la solution : Arche Y m'aide.
Hervé Le Tellier et Olivier Salon, tous deux complices, membres de l'Oulipo et ayant fréquenté de près les mathématiques, font jouer le public avec des Chicagos sur des noms de mathématiciens pour les trente ans de Tangente. Un moment ludique, enlevé, drôle, enjoué !
Le jeu de la vie de John Conway – Jean-Paul Delahaye
(Amphithéâtre, 16h30)
Né dans l'esprit du mathématicien John Conway en 1970, l'automate cellulaire du Jeu de la vie définit un monde imaginaire. La physique de cet univers a été soigneusement étudiée et continue de l'être par quelques milliers de passionnés. La construction de configurations initiales aux propriétés particulières (par exemple engendrer un à un les nombres premiers, ou calculer le nombre π) a mis à notre disposition un répertoire singulier de formes dynamiques. Elles sont les habitants d'un univers parallèle, autonome et mystérieux. Leurs combinaisons et les mouvements auxquels elles donnent naissance nous apparaissent comme les manifestations d'une vie différente de celle que nous connaissons sur terre. Peut-être le rêve des formes de nos ordinateurs ?
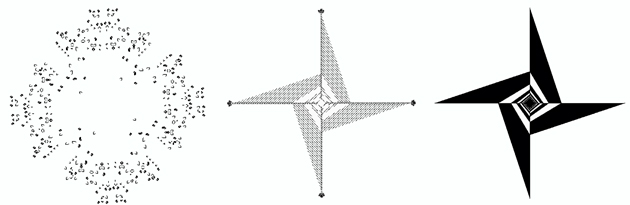
L'image représente trois étapes (à des échelles différentes) du développement d'une configuration du jeu de la vie qui calcule le nombre π. La population à la génération n est asymptotiquement (π - 2)n2/720. Autrement dit : si m est le nombre de cellules vivantes à l'étape n, alors 720m/n2 + 2 est une approximation de π. La configuration a été créée par Dean Hickerson.
