La méthode PERT
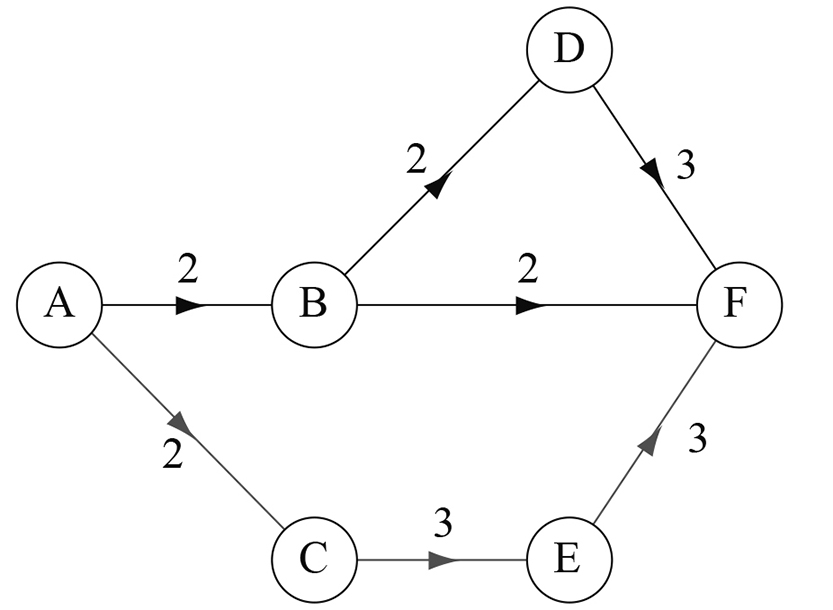En 1958, en pleine guerre froide, la marine américaine cherchait à développer le plus rapidement possible le système Polaris de sous-marins lanceurs de missiles nucléaires. Le projet comportait deux cent cinquante fournisseurs, sans compter les sous-traitants. Pour coordonner le tout, la marine mit alors au point une méthode reposant sur la théorie des graphes, la méthode PERT (Program Evaluation and Review Technique). Elle consiste à décomposer le projet en un certain nombre de tâches, chacune devant être exécutée après une autre (ou pas) et ayant une certaine durée. Cela donne un graphe fait de nœuds (début et fin des tâches) et d'arêtes (accomplissement des tâches avec durée). L'idée de PERT est d'y repérer le plus long trajet allant de l'état initial (A sur la figure) à l'état final (F sur la figure), qui est ici repéré en rouge.
Ce trajet donne le temps minimal pour finir le projet et fait ressortir les processus les plus sensibles. Avec cette méthode, le projet Polaris fut achevé en 1960, avec une avance de cinq ans sur les prévisions initiales !
De même, grâce à la méthode PERT, du discours de John Kennedy annonçant le projet américain d'envoyer un homme sur la lune (25 mai 1961) à l'atterrissage d'Apollo 11 sur notre satellite (20 juillet 1969), il ne s'écoulera que huit années !
Minimiser des sommes de valeurs absolues
La fonction valeur absolue f (notée par f (x) = | x |) n'est pas dérivable en son minimum (f (0) = 0). Sa dérivée est constante ailleurs, sautant de –1 à +1 en x = 0. De même, la fonction g qui, à x, associe | x – a | prend son minimum (g (a) = 0) en x = a, en laquelle elle n'est pas dérivable. Comment peut-on minimiser des sommes de valeurs absolues de différences ? Réfléchissons avec la fonction h (x) = (| x – a | + | x – b |),
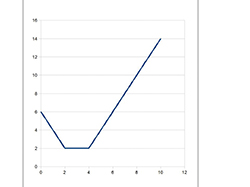
où a < b. Cette fonction continue est affine par morceaux : elle présente une première demi-droite de pente –2 pour toute valeur de x inférieure à a, un segment horizontal (d'ordonnée b – a) entre a et b, et une demi-droite de pente 2 pour x > b. Le minimum est réalisé en tout point de l'intervalle [a, b] (sur le graphique, a = 2 et b = 4).
On raisonne de même pour la somme de plusieurs valeurs absolues. Il suffit d'ordonner les paramètres (ici, a, b et c) de manière croissante (a < b < c) et de considérer la fonction j (x) = (| x – a | + | x – c |) + | x – b |. La première parenthèse prend son minimum (à savoir c – a) pour toute valeur appartenant à [a, c]. Le second terme (toujours positif ou nul) prend son minimum (valeur 0) en x = b, qui devient alors le seul minimum global de la fonction.
La métrique qui justifie la médiane
Dans une statistique donnée x1, x2… xn, comment résumer les n valeurs numériques au moyen d'une constante ? Remplacer une suite de nombres variables par un nombre unique a induit une nouvelle statistique, composée des résidus (ou erreurs) ei = xi – a. Pour un résumé a « bien choisi », central, certaines de ces erreurs sont positives, d'autres négatives. Le « bon choix » de a doit correspondre à un critère de minimum global des erreurs. On convient alors de rendre toutes les erreurs positives et de les agréger. Une façon simple de procéder est de considérer comme erreur totale ET la somme des valeurs absolues des erreurs. On procède au classement des observations par ordre croissant. On regroupe les termes deux par deux en considérant une suite d'intervalles emboîtés, en réunissant le premier et le dernier, le deuxième et l'avant-dernier, et ainsi de suite. Dans le cas impair, il existe un terme central isolé, qui correspond au minimum. Dans le cas d'un nombre pair d'observations, il existe deux observations « centrales ». Le minimum est alors réalisé pour toute valeur comprise entre ces deux valeurs. C'est ainsi que l'on retrouve la notion de médiane ! Ainsi, la métrique des valeurs absolues peut conduire à la non-unicité de ce paramètre de centralité.