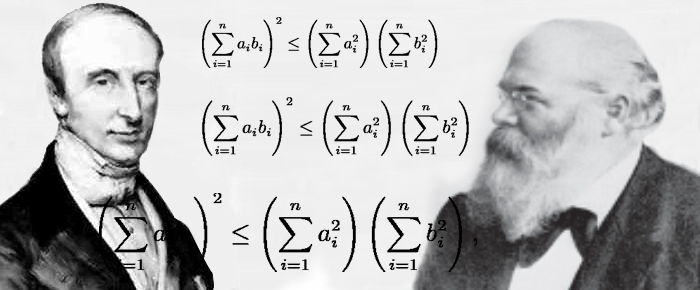Optimisation
L'activité humaine est soumise à des contraintes de toutes sortes : matérielles, humaines, financières, spatiales, temporelles… Cette limitation des ressources explique qu'une grande partie des « mathématiques appliquées » consiste à optimiser un critère sous certaines contraintes.
Ce dossier ciblé propose d'explorer une facette méconnue et non technique de l'optimisation : oui, sans machinerie analytique sophistiquée, avec seulement une bonne compréhension de concepts algébriques ou géométriques simples, on peut déjà obtenir des résultats étonnants !
Ce dossier ciblé propose d'explorer une facette méconnue et non technique de l'optimisation : oui, sans machinerie analytique sophistiquée, avec seulement une bonne compréhension de concepts algébriques ou géométriques simples, on peut déjà obtenir des résultats étonnants !
LES ARTICLES
Sans dériver - L'optimisation pour tous !
Hervé Lehning
Optimisation et dérivation des fonctions sont deux questions liées... mais il est parfois possible de s'en passer, en algèbre comme en géométrie. Quelques exemples algébriques élémentaires nous convaincront que le second degré est souvent plus subtil qu'il en a l'air...
Un art de géomètres
Élisabeth Busser
La géométrie a ses secrets, elle permet souvent de résoudre ses problèmes d'extremum dans recourir à l'analyse ou à l'algèbre. C'est aussi l'occasion de revisiter quelques résultats classiques de la géométrie du triangle.
Problèmes d'optimisation en région montagneuse
Jacques Bair
D'un point de vue géométrique, optimiser une fonction de deux variables consiste à localiser des points privilégiés sur sa représentation graphique : les points « les plus hauts » et « les plus bas ». Cette recherche peut être illustrée par l'étude d'un… paysage montagneux.
En bref : D'autres optimisations
Daniel Justens et Hervé LehningLes procédés d'optimisation se cachent parfois dans d'autres sujets. En voici quelques exemples