On a tous déjà vu, dans une fête foraine, ce jeu où il faut recouvrir totalement un grand disque avec six petits disques identiques. C'est le jeu des palets. Le forain fait une démonstration rapide ; ça a l'air facile. Vous avez droit à trois tentatives, vous essayez et… en général, vous perdez.

Supposons que les petits disques aient un diamètre de 10 cm. Quel est le diamètre minimal du grand disque pour qu'il puisse être recouvert et quelle doit être alors la disposition des petits disques pour le recouvrir totalement ? La première idée est de placer les petits disques régulièrement « en rosace ». Le diamètre du grand disque est alors précisément égal à 10√3, soit environ 17,32 cm. Peut-on faire mieux ? Eh bien oui, avec une disposition moins régulière.

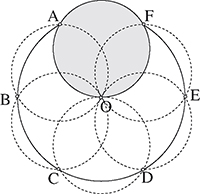
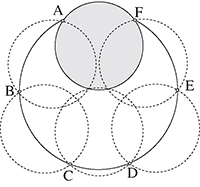
Avec cette disposition, qui présente un seul axe de symétrie, le grand disque a un diamètre d'environ 17,98 cm. Le mathématicien hongrois Károly Bezdek a démontré qu'elle était optimale.

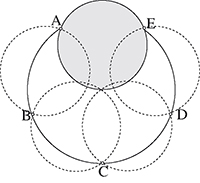
Une version anglo-saxonne de ce jeu existe avec cinq disques. Ici encore, la disposition optimale n'est pas régulière. Le diamètre du grand disque est égal à environ 16,41 cm.

Recouvrement d'un carré

Posons le même problème en remplaçant le grand disque par un carré, les petits disques ayant toujours 10 cm de diamètre. Avec deux disques, vous trouverez facilement la longueur minimale du côté du carré.

1. Quelle est cette longueur minimale du côté du carré recouvert par deux disques ?

Avec trois disques, le problème se complique un peu. Vous vous convaincrez facilement que le côté du carré est légèrement plus petit que le diamètre des disques. Mais l'écart est faible…

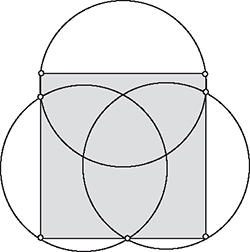
2. L'écart est-il supérieur ou inférieur à 1 % de la longueur du côté du carré ?