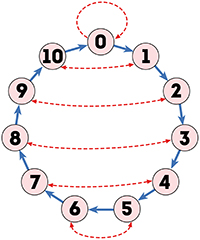
Les critères de divisibilité peuvent sembler magiques, comme ceux par 7 et par 11. Prenez un nombre quelconque et jouez à ce jeu de l'oie :
1. Commencez par la case 0,
2. En suivant les flèches bleues, déplacez-vous d'autant de cases que le premier chiffre du nombre,
3. Parcourez la flèche rouge, qui vous fera aller en avant ou en arrière d'un certain nombre de cases,
4. À partir de cette case, répéter les opérations 2 et 3, jusqu'à extinction des chiffres (si un chiffre est 0, n'appliquez que la règle 3.),
5. Si le parcours du dernier chiffre tombe sur la case de départ 0, c'est que le nombre choisi était divisible par 7.
 Ainsi, à partir de 805, on part de zéro, on parcourt huit flèches bleues ; avant de passer au chiffre suivant, on parcourt la flèche rouge, qui nous amène à la case 3. Le chiffre suivant est 0, donc on n'avancera pas, mais on devra parcourir la flèche rouge, qui nous ramène à la case 2. Enfin, le dernier chiffre est 5, donc on parcourt hardiment cinq flèches ; on tombe sur la case départ : 805 est divisible par 7.
Ainsi, à partir de 805, on part de zéro, on parcourt huit flèches bleues ; avant de passer au chiffre suivant, on parcourt la flèche rouge, qui nous amène à la case 3. Le chiffre suivant est 0, donc on n'avancera pas, mais on devra parcourir la flèche rouge, qui nous ramène à la case 2. Enfin, le dernier chiffre est 5, donc on parcourt hardiment cinq flèches ; on tombe sur la case départ : 805 est divisible par 7.
Vous l'aurez deviné, tout se passe modulo 7 : les cases numérotées de 0 à 6 représentent les restes de division d'entiers par 7, chaque flèche bleue représente l'addition de 1 modulo 7, chaque flèche rouge symbolise le reste de puissances de 10 modulo 7. Ainsi, 805 = ((8 × 10 + 0) × 10) + 5. À vous de traduire cela modulo 7 !
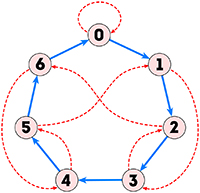
En connaissant mieux le fonctionnement de ce petit jeu, vous pourrez confectionner d'autres graphes de divisibilité qui respectent les mêmes règles, par exemple celui de la divisibilité par 11…