Le recours au calcul intégral pour le calcul d'aires est un grand classique, comme l'illustre le précédent article. Le résultat fondamental du calculus, qui unit la recherche de primitives et le calcul d'intégrales définies, permet très souvent la résolution élégante de problèmes de ce type. Mais ce n'est pas toujours le cas ! Ainsi, le calcul de l'aire du cercle se révèle particulièrement lourd en coordonnées cartésiennes ; le passage aux coordonnées polaires est alors d'un apport esthétique et pratique considérable. Mais ce n'est pas tout. Cette transformation permet aussi la résolution de problèmes de calculs d'intégrales de fonctions considérées comme non intégrables en coordonnées cartésiennes…
Vive la trigonométrie !
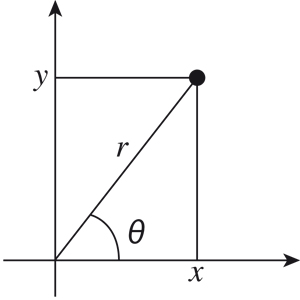Dans un système de coordonnées polaires, on identifie un point du plan de coordonnées cartésiennes (x, y) en joignant ce point à l'origine, en mesurant l'angle θ (dans [0, 2[) entre ce segment et l'horizontale, et également la distance r > 0 entre le point et l'origine. Les relations traduisant le passage d'un système de coordonnées à l'autre sont alors x = r cosθ et y = r sinθ.
Comment calculer l'aire S d'un cercle C de rayon R ? En coordonnées cartésiennes, on intègre la fonction unité sur ...
Lire la suite