
L'énoncé de la fameuse loi des aires énoncée par Johannes Kepler (1571–1630) est le suivant : les planètes balaient des surfaces égales en des temps égaux. Pour l'expliquer, on l'accompagne en général d'un schéma tel que celui-ci.
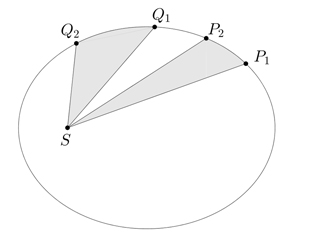
Dans ce schéma, le point S désigne le Soleil. L'aire balayée par la planète entre les points P1 et P2 est l'aire du domaine limité par les segments [SP1] et [SP2] et par l'arc de trajectoire limité par P1 et P2. La loi des aires dit que si le même temps t est requis par la planète pour aller de P1 à P2 que pour aller de Q1 à Q2, alors les aires des domaines SP1P2 et SQ1Q2 sont égales. Spectaculaire, cette loi a considérablement renouvelé l'idée que l'on se faisait de l'« ordre céleste ». En accordant une place éminente au Soleil aux dépens de la Terre, elle a aussi contribué à déloger notre planète du statut central qui était le sien dans les descriptions antiques du cosmos.
Un tour de force
Kepler lui-même n'a pas démontré les lois éponymes, il les a seulement énoncées à partir des observations dont il disposait. Il faudra attendre près d'un siècle pour qu'une preuve soit apportée, ... Lire la suite
