
Le mot « convexe » provient du latin convexus, dont le sens premier est « bombé, courbé et arrondi en dehors » ; on dit parfois qu’une courbe convexe « tourne sa concavité vers le haut », au contraire d’une courbe concave dont « la concavité est dirigée vers le bas ».
En géométrie, on étudie depuis longtemps les polygones convexes dans le plan et les polyèdres convexes dans l’espace ; un polygone est qualifié de « convexe » lorsque l’un quelconque de ses côtés laisse toute la figure d’un même côté par rapport à lui. Plus généralement, on s’intéresse aux ensembles convexes qui, intuitivement, sont caractérisés par le fait qu’ils sont « dépourvus de creux ».
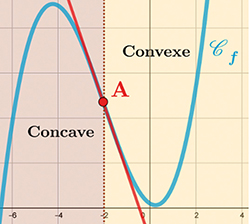
Une courbe possédant une partie convexe et une partie concave.

Exemple de polygones.
Les prémisses d’une théorie
Les premières traces de la convexité remontent à l’Antiquité, essentiellement chez des savants grecs. Ainsi, le quatrième livre des Éléments d’Euclide s’intéresse aux polygones (convexes ou non) du plan, à leur construction à la règle et au compas, ainsi qu’à leur inscription dans un cercle. Les trois derniers livres sont consacrés à la géométrie dans l’espace, avec une attention particulière pour les polyèdres et, en fin d’ouvrage, pour ... Lire la suite
