
Plier une feuille en deux, rien de plus simple ! Construire le milieu d’un segment via l’origami n’a donc rien de bien méchant et s’avère déjà plus simple que dans la classique géométrie à la règle et au compas. Partant d’une feuille carrée de côté 1, on peut donc obtenir une longueur de 1/2. Peut-on obtenir d’autres longueurs ? Plier une feuille en trois semble déjà un peu plus délicat. Par essais successifs, on peut avoir l’impression de s’en sortir raisonnablement, mais une construction exacte serait plus satisfaisante.
Pas besoin de se plier en quatre !
Prenez une feuille carrée et marquez le milieu du côté supérieur. Ramenez maintenant le coin inférieur droit sur le milieu du côté supérieur et admirez le travail.
Pour faciliter l’étude de la figure obtenue, on peut introduire quelques notations, comme indiqué sur le dessin ci-dessous.
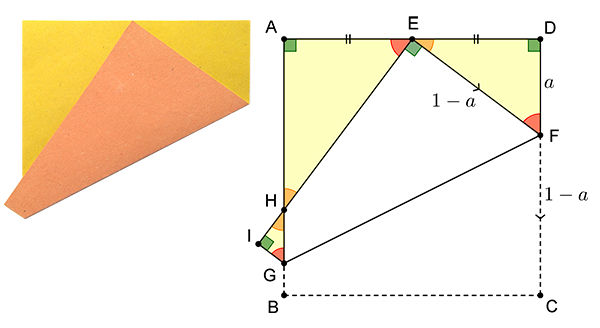
Un pli si simple et si riche à la fois…
En considérant les angles, on peut déjà remarquer que les trois triangles DEF, AHE et IGH sont semblables. Intéressons-nous maintenant au triangle rectangle DEF obtenu en haut à droite.
Posons DF = a.
Par pliage, on a EF = FC = 1 ‒ a.
D’après le théorème de Pythagore, on ... Lire la suite
