L’origami permet d’obtenir des constructions impossibles à la règle et au compas seuls, comme la duplication du cube ou la trisection de l’angle (voir La Géométrie de la règle et du compas, Bibliothèque Tangente 78, 2022). Le plus emblématique des problèmes de construction de l’Antiquité, la quadrature du cercle, c’est-à-dire la construction d’un carré d’aire π à partir d’un segment de longueur 1, reste inaccessible via l’origami.
Mais il est amusant d’essayer d’en obtenir une « bonne approximation ».
Haga, Haga, Haga, et pi voilà !
Partons donc d’un carré ABCD.
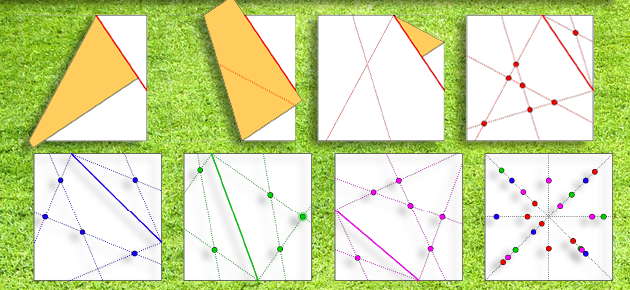
En ramenant le point D sur le milieu de [AB], le premier théorème de Haga (voir article «Le pli de Haga ») nous donne le point E de [BC] tel que CE = 1/3.
En ramenant D sur E, on obtient le point F de [AB] tel que BF = 7/9 (car BF = g (1/3) + b (1/3) dans les notations de l’article « Le pli de Haga »).
En ramenant maintenant C sur F, on obtient le point G de [BC] tel que BG = 16/81 (ou f (7/9) dans les notations de l'article « Le pli de Haga »). On double cette longueur en construisant H ... Lire la suite
