
Un entrelacs (ou nœud celtique) est un ensemble fini de courbes fermées entrelacées (les brins), enchevêtrées sans se couper. Ces objets sont à la base de nombreux motifs ornementaux dans différentes cultures. On représente en général un entrelacs par l’une de ses projections sur un plan, dans une position telle (c’est toujours possible) que les croisements des brins dans cette représentation n’impliquent que deux courbes, avec des tangentes distinctes. On indique les passages « dessus, dessous » en effaçant, lors du croisement, le tracé de chaque lacet qui passe en dessous.
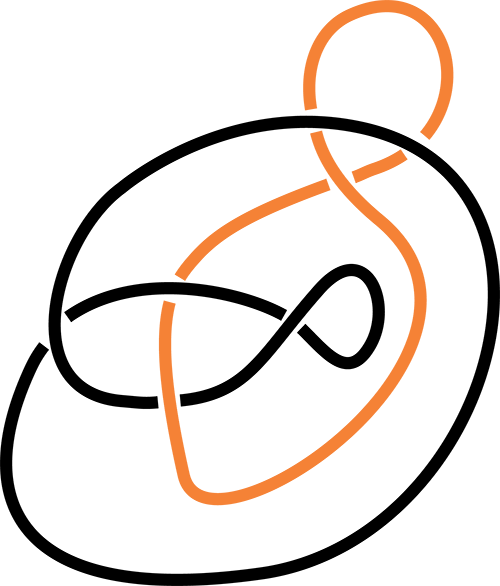
Entrelacs comportant deux brins.
Un graphe, quant à lui, est un schéma plan formé de points, les sommets, qui peuvent (ou non) être reliés entre eux par des traits, les arêtes, le plus souvent représentées par des segments. On l’appelle graphe planaire quand on peut trouver une représentation où aucune arête n’en croise une autre.
Une relation réciproque, mise à jour à la fin du XIXe siècle, entre les graphes planaires et les entrelacs permet d’étudier plus facilement ces derniers.
De l’entrelacs au graphe…
À partir du diagramme de l’entrelacs, on peut définir un graphe associé et, en retour, tout graphe planaire nous permettra de dessiner un entrelacs ... Lire la suite
