
Pour répondre à la question, analysons un graphe à n sommets comprenant m arêtes. Notons di le degré du sommet i, c’est-à-dire le nombre d’arêtes qui partent de ce sommet. La somme des degrés des sommets vaut 2m car chaque arête (i, j) est comptabilisée à chacune de ses extrémités i et j. L’inégalité de Cauchy‒Schwartz donne :
Il faut maintenant un petit peu d’astuce. Additionner les carrés des degrés des sommets, c’est compter le degré de chaque sommet autant de fois qu’il y a d’arêtes qui partent de ce sommet. Une autre façon d’obtenir ce total est d’additionner des sommes di + dj pour tous les couples (i, j) correspondant à une arête du graphe.
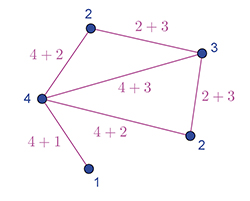
Ce graphe contient deux triangles.
La somme des carrés des degrés (22 + 32 + 22 + 42 + 12) est égale à la somme des sommes indiquées en rose sur chaque arête : le 4 apparaît bien quatre fois dans les sommes roses (ce qui donnera 42), le 3 trois fois (ce qui donnera 32)…
Regardez maintenant une arête (i, j). Si le graphe ne contient aucun triangle, les extrémités des di ‒ 1 arêtes adjacentes à l’arête (i, j) issues de i sont toutes différentes des dj ‒ 1 extrémités des ... Lire la suite gratuitement
