
Un ensemble E de points, du plan ou de l’espace, est dit convexe si, pour tout couple de points (A, B) appartenant à E, le segment de droites d’extrémités A et B y appartient aussi.
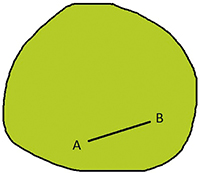
Domaine convexe : pour tout couple de points (A, B) de E,
le segment [AB] est tout entier inclus dans E.
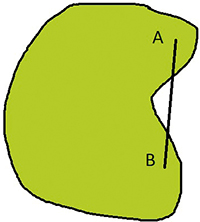
Domaine non convexe : il existe au moins deux points A et B
tels que le segment [AB] ne soit pas totalement compris dans E.
Cette notion a nécessité beaucoup de temps pour être formalisée d’un point de vue mathématique. Bien que présente de manière implicite dans les Éléments d’Euclide (vers ‒300), en particulier à propos des polygones ou des polyèdres, ou dans les travaux d’Archimède (IIIe siècle avant notre ère) ou ceux de Ptolémée (IIe siècle avant notre ère, voir article « Une inégalité méconnue, celle de Ptolémée »), il faut attendre les travaux de Hermann Minkowski au tournant des XIXe et XXe siècles pour avoir des définitions précises.
C’est au cours des années 1960 que la géométrie convexe prend son essor, en particulier en raison de ses applications en calcul des probabilités et en optimisation (voir notre dossier ... Lire la suite gratuitement
