
Pour un quadrilatère inscrit dans un cercle, le produit des longueurs des diagonales est égal à la somme des produits des longueurs de ses côtés opposés.

On a AC × BD = AB × CD + AD × BC.
Ce théorème contient en fait celui de Pythagore : prenez un rectangle de longueurs de côtés a et b et de longueur de diagonale c ; il s’agit bien d’un quadrilatère inscriptible, et le théorème de Ptolémée affirme que c × c = a × a + b × b. C’est la relation de Pythagore !
Ptolémée a démontré son théorème par la géométrie classique des triangles semblables et le théorème de l’angle inscrit, selon lequel des angles inscrits dans un cercle interceptant le même arc sont égaux (voir Le Cercle, Bibliothèque Tangente 36, 2009 et Les Angles, Bibliothèque Tangente 53, 2015). Ici, nous allons l’obtenir comme cas d’égalité dans une inégalité, tout d’abord en utilisant le plan complexe, c’est-à-dire le plan euclidien habituel où chaque point est repéré par son affixe (ses coordonnées vues comme un nombre complexe).
Claude Ptolémée, le père de la géographie
Claude Ptolémée est un astronome grec qui a vécu à Alexandrie. Né vers l’an 100, il meurt vers 168. On connaît peu de choses de sa vie. À la recherche d’une compréhension rationnelle du monde qui l’entoure, et plus généralement de l’univers, il est considéré comme le père de la géographie.
Ptolémée est l’auteur de plusieurs livres dont deux, l’un en géographie et l’autre en astronomie, ont exercé une grande influence sur les sciences en Occident au Moyen Âge. En mathématiques, il étudie la géométrie, en particulier les projections, ainsi que la trigonométrie. Il est parfois difficile de distinguer son apport de celui d’Hipparque, qui vécut au IIe siècle avant notre ère et qui est, lui, considéré comme le père de la trigonométrie.

Ptolémée, tel que représenté par Girolamo Mocetto au début du XVIe siècle.
Une première démonstration
La relation de Ptolémée fait penser à la relation d’Euler,
qui permet de démontrer que si un point D appartient à la hauteur issue de A d’un triangle ABC et à la hauteur issue de B, alors il appartient aussi à celle issue de C.
Cependant, il s’agit ici de produits scalaires, pas de produits des longueurs…
Par contre, la relation similaire (d ‒ a)(c ‒ b) + (d ‒ b)(a ‒ c) + (d ‒ c)(b ‒ a) = 0 est valable dès que le produit est distributif et commutatif, en particulier donc aussi dans l’ensemble des nombres complexes.
Les nombres complexes a, b, c et d étant respectivement les affixes des points A, B, C et D, et en écrivant la relation précédente sous la forme
(c ‒ a) (d ‒ b) = (b ‒ a)(d ‒ c) + (d ‒ a)(c ‒ b),
on obtient, par l’inégalité triangulaire,
| c − a | × | d − b | ≤ | b − a | × | d − c | + | d − a |× | c − b | ,
ce qui s’écrit aussi :
AC × BD ≤ AB × CD + AD × BC.
C’est l’inégalité de Ptolémée, valable pour quatre points quelconques du plan.
Quel est alors le cas d’égalité ? Pour simplifier, on suppose les points distincts et non alignés.
On a l’égalité dans une inégalité triangulaire du type |u + v| ≤ |u| + |v| lorsque les nombres complexes u et v ont même argument (voir Les Nombres complexes, Bibliothèque Tangente 63, 2018). Dans le cas qui nous intéresse, on a donc l'égalité si (b ‒ a)(d ‒ c) et (d ‒ a)(c ‒ b) ont même argument, ce qui s’écrit aussi
soit
Le théorème de l’angle inscrit (voir notre dossier dans Tangente 178, 2017) nous dit que la condition nécessaire et suffisante est que A, B, C et D soient sur un même cercle dans cet ordre ; on a donc obtenu le théorème de Ptolémée.
Trois jolies applications
Dans un triangle ABC, si M est un point intérieur et si H, K et L sont les projetés orthogonaux de M respectivement sur les côtés (BC), (AC) et (AB),
on a MA + MB + MC ≥ 2(MH + MK + ML). C’est l’inégalité d’Erdős‒Mordell.
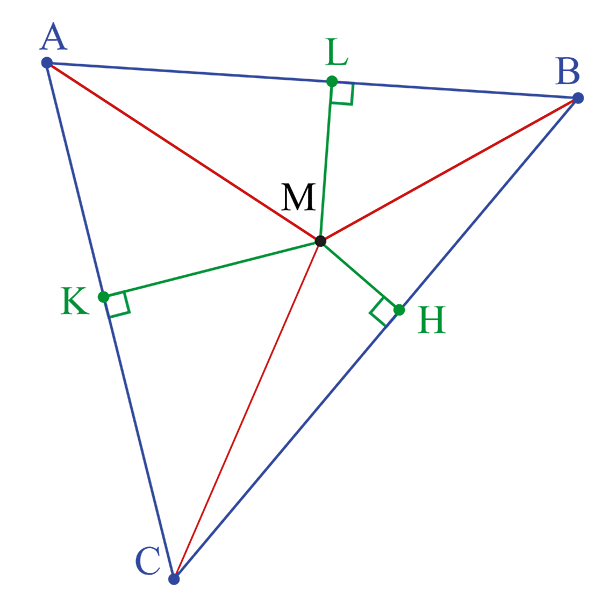
Ce résultat a été conjecturé en 1935 par le Hongrois Paul Erdős (1913‒1996) et démontré en 1937 par le mathématicien américano-britannique Louis Mordell (1888‒1972), plus connu pour ses résultats en théorie des nombres. Alors que l’énoncé est élémentaire, la démonstration donnée par Mordell ne l’était pas du tout (voir article « Les richesses de l'inégalité triangulaire »). Depuis, des preuves plus simples ont été données, entre autres en utilisant l’inégalité de Ptolémée.
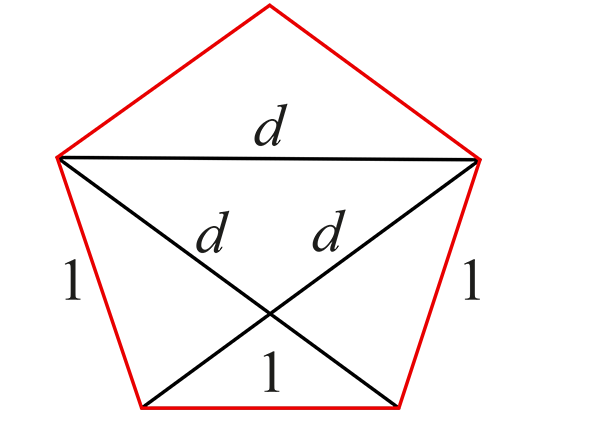
Saviez-vous que les trois diagonales d’un pentagone régulier ont même longueur ? Les diagonales d’un pentagone régulier convexe de côté 1 ont en effet pour longueur le nombre d’or. Pour s’en convaincre, on remarque que le quadrilatère indiqué dans la figure est inscriptible. Donc, d’après la relation de Ptolémée, d 2 = d + 1, qui est l’équation définissant le nombre d’or (voir notre dossier dans Tangente 203, 2022) ! Pour des polygones ayant un plus grand nombre de côtés, Ptolémée nous donne des relations entre les longueurs des diverses diagonales.
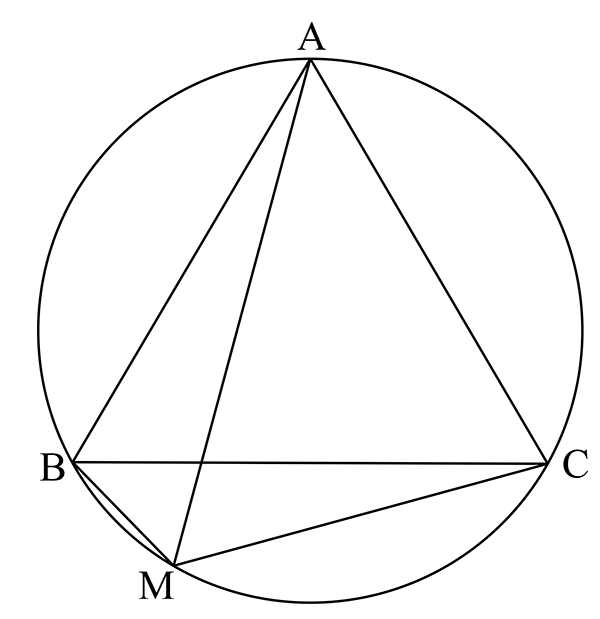
Regardez maintenant un triangle équilatéral ABC et son cercle circonscrit. Un point M appartient à ce cercle si, et seulement si, l’une des distances MA, MB et MC est égale à la somme des deux autres ! En effet, la relation de Ptolémée se simplifie par la longueur commune des côtés du triangle.
Une leçon à tirer de tout ceci est que la condition d’égalité est au moins aussi importante que l’inégalité elle-même !
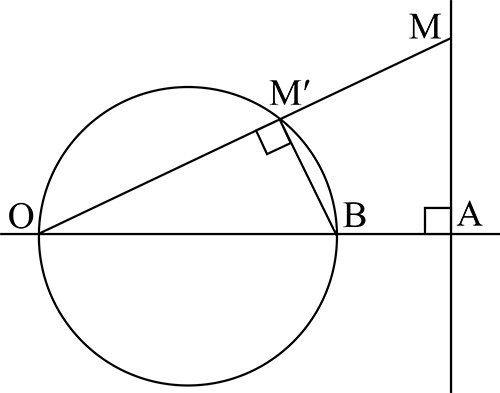
Une démonstration par inversion
Les triangles OM’B et OAM étant semblables, on a
Une inversion de centre O et de rapport 1 transforme tout point M en un point M′ de la droite (OM) défini par la relation d’où le nom de cette transformation.
L’image d’une droite par une inversion est un cercle.
Une propriété remarquable est que si N′ est l’image de N, alors :
On a aussi le fait que l’image d’une droite ne passant pas par le centre d’inversion est un cercle passant par ce centre.
Soient alors A′, B′ et C′ les images respectives de A, B et C par l’inversion de centre D et de rapport 1. Avec les expressions des longueurs images :
et
l’inégalité de Ptolémée AC × DB ≤ AB × DC + BC × DA s’obtient par la simple application de l’inégalité triangulaire A′C′ ≤ A′B′ + B′C′ !
Il y a égalité si, et seulement si, A′, B′ et C′ sont alignés, dans cet ordre, ce qui est équivalent au fait que A, B, C et D sont cocycliques ou alignés, dans cet ordre. L’inégalité triangulaire conduit à des conséquences inattendues !
Références
• 1000 challenges mathématiques : géométrie. Mohammed Aassila, Ellipses, 2018.
• Les transformations. Bibliothèque Tangente 35, 2009.


