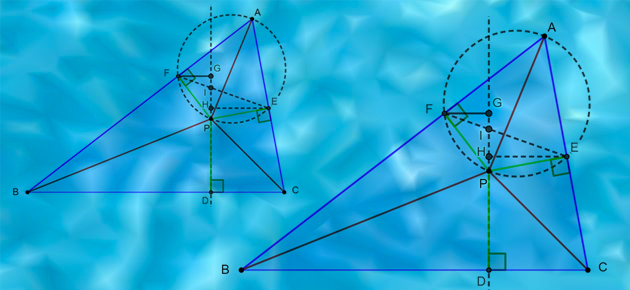
Comparaison : une origine géométrique

Comparer des quantités est une activité des plus naturelles : qui possède le moins d’objets, ou le plus grand champ ? Avant de connaître toutes les ficelles mathématiques qui permettent d’augmenter la superficie de son terrain ou un préceux capital, il est utile de revenir aux origines géométriques de la question, afin de bien visualiser les quantités en jeu. L’inégalité du triangle et l’astuce de Didon nous étonnent encore aujourd’hui par leur fécondité.

LES ARTICLES

Les richesses de l’inégalité triangulaire

Élisabeth Busser

Qui dit « inégalités » pense souvent arithmétique ou algèbre. Mais les inégalités occupent aussi le domaine géométrique ! La plus fameuse d’entre elles, la célèbre inégalité triangulaire, recèle encore plus d’un tour dans son sac.

Le problème de Didon

Guy Porthault

Le disque est, à périmètre donné, la figure ayant la plus grande aire. Ce résultat, qui a été popularisé grâce à une astuce que l’on prête à Didon, la fondatrice et première reine de Carthage, est le « théorème isopérimétrique ». Il est à l’origine de nombreuses inégalités plus générales.

Une inégalité méconnue, celle de Ptolémée

Robert Ferréol

Le mathématicien, géographe et astronome grec Claude Ptolémée a découvert, au IIe siècle de notre ère, un théorème concernant les quadrilatères inscrits dans un cercle. Son résultat est certes beaucoup moins célèbre que celui de son compatriote Pythagore, mais il est tout aussi beau.

En bref : La convexité, facile à visualiser

Daniel Lignon