
La théorisation des produits financiers à risque pose problème. Les premières tentatives de modélisation sophistiquées datent de la toute fin du XIXe siècle et sont dues aux travaux du mathématicien français Louis Bachelier (1870 ‒1946) dont les résultats demeurèrent discrets voire méconnus jusqu’à ce que Benoît Mandelbrot les sorte de l’ombre.
Les limites de la modélisation en loi normale
Prenons par exemple les croissances « journalières » – c’est-à-dire sur des intervalles de temps, variables, entre deux journées boursières consécutives – observées récemment pour le CAC40 et illustrées dans le graphique ci-dessous. On en calcule aisément moyenne (0,13 %) et écart-type (0,622 %), ce qui nous permet, sous hypothèse de normalité, de construire un intervalle comprenant en théorie 99 % des observations : il s’agit de l’intervalle [-1,48 % ; 1,73 %].
Pourtant, en réalité, 3% des observations sont extérieures à cet intervalle, soit trois fois plus que prévu ! C’est un fait bien connu : les distributions de rendements observés de produits financiers ne suivent pas une loi normale (représentée par une courbe de Gauss en forme de cloche) mais sont leptokurtiques (voir encadré).
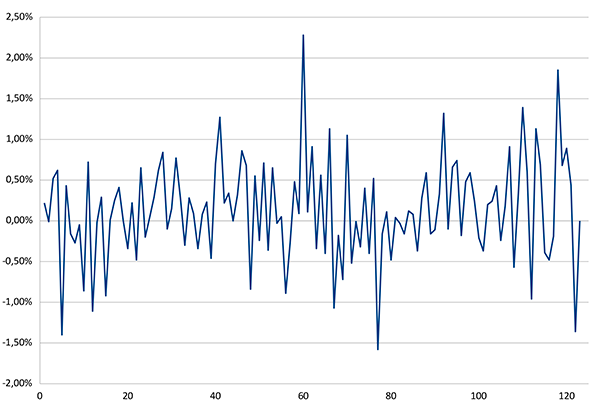
Croissances journalières pour le CAC40 du 1er novembre 2023 au 22 avril 2024.
Différentes distributions
Une distribution leptokurtique, du ... Lire la suite
références
• Pour en savoir plus sur les modèles concurrents et les aspects techniques de la performance de la mesure multifractale : L’introduction des mesures multifractales en finance, Daniel Justens, Les nouveaux défis de la statistique, Bibliothèque Tangente n°86, 2024.
