Définir la dimension : pas si simple…
Selon Euclide, la dimension d’un objet est le nombre de paramètres nécessaires pour le décrire : une droite est de dimension 1, tandis qu’un plan est de dimension 2. Cela s’est matérialisé avec l’introduction des coordonnées, suite aux travaux de Descartes au XVIIe siècle.
Les courbes et les surfaces possèdent aussi une dimension. Une courbe classique, comme un cercle, une parabole ou une sinusoïde est, de manière assez évidente, un objet de dimension 1. Ainsi, une origine et une unité de longueur ayant été choisies, tout point se représente avec un seul paramètre : l’abscisse curviligne. Sur une sphère, deux paramètres permettent de repérer n’importe quel point : ce sont la longitude et la latitude, utilisées pour désigner un lieu à la surface de la Terre. La sphère est donc de dimension 2 tandis que la boule, intérieur de la sphère, est, elle, de dimension 3.
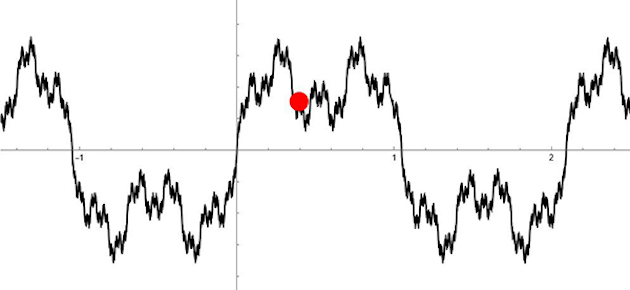
L’apparition, à la fin du XIXe siècle, d’« objets étonnants » comme le graphe de la fonction de Weierstrass, le flocon de von Koch (voir article « L'homme des brisures ») ou le triangle de Sierpiński ont remis en cause cette notion simple de dimension.
Diverses définitions ont été proposées au cours du XXe siècle pour ... Lire la suite gratuitement
