
Pendant des siècles, le principal affrontement qui se déroula sur les terres de la géométrie concerna le droit et le courbe. Le premier portait en étendard les certitudes offertes par des formules connues et utilisées depuis des temps immémoriaux telles que celles exprimant l’aire des polygones. Le second lui opposait un grand nombre de problèmes délicats qui allaient jusqu’à questionner la définition même d’une longueur.
Dès l’Antiquité pourtant, Archimède avait jeté les bases d’un gentlemen’s agreement entre les deux, notamment dans le cadre du calcul du nombre π, rapport de la circonférence d’un cercle à son diamètre.
Le courbe dompté par le droit
On peut encadrer la mesure de la circonférence d’un cercle en la minorant par le périmètre d’un polygone régulier inscrit et en la majorant par celui d’un polygone régulier circonscrit. (Ici, les polygones ont douze côtés.) En trouvant une formule explicite pour le périmètre de polygones réguliers au nombre de côtés de plus en plus grand, Archimède a obtenu une méthode d’approximation de π qui a fait autorité pendant deux millénaires.

La courbure d’un cercle empêchait d’en calculer directement la circonférence, mais le recours à des approximations de plus en plus fines par des polygones réguliers inscrits et circonscrits permettait de surmonter cette limitation.
Certes, le prix à payer pour ramener ainsi le courbe au droit était un recours à l’infini qui posait à son tour de nouvelles questions qui mettraient un certain nombre de siècles à être réglées pour de bon. Les derniers soubresauts de cette bataille avaient toutefois cessé au XIXe siècle, où l’infini avait été définitivement dompté par les travaux de Augustin Louis Cauchy, Bernard Bolzano, Richard Dedekind, et surtout Georg Cantor.
Les germes d’une révolution
L’apaisement avait été obtenu d’une façon qui portait malgré tout en elle les germes d’une révolution. D’abord invisibles en raison de leur présentation extrêmement théorique autant que de leur caractère apparemment anecdotique, des monstres mathématiques naquirent au début du XXe siècle, silencieusement, avant que Mandelbrot finisse par les sortir de leur tanière érudite. Ils avaient pour nom courbe de Takagi, tapis de Sierpiński ou encore courbe de Peano. Il s’agissait de curiosités dont l’élaboration avait été rendue possible par le développement de nouvelles perspectives.
L’étude fine de l’infini ayant alors permis de disposer d’une description mathématiquement parfaitement satisfaisante de la structure d’une banale ligne droite, il avait été possible non seulement de la tordre comme on savait déjà le faire, mais aussi de la briser en une infinité de morceaux, pour constituer des formes radicalement nouvelles, sans perdre la capacité de décrire le résultat obtenu.
L’exemple sans doute le plus célèbre de droite ainsi malmenée est le flocon de von Koch (voir encadré), l’un des tous premiers exemples de ce que Mandelbrot appellerait par la suite un fractal pour insister sur l’idée de fracture qui est à l’œuvre dans une telle construction.
Le flocon de von Koch
Proposé par le mathématicien suédois Helge von Koch en 1904, le flocon éponyme est une courbe limite. On part d’un segment initial, dont on retire le tiers central pour le remplacer par deux côtés de même longueur que lui. On répète ensuite la même opération pour chacun des quatre petits segments ainsi obtenus, et ainsi de suite. La courbe finale est de longueur infinie, tout en ne limitant (avec le segment initial) qu’une aire finie, calculée par von Koch comme égale à (le segment initial étant pris comme unité).

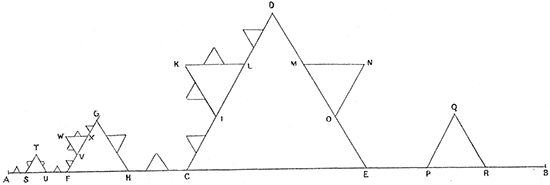
La construction du flocon, telle qu’elle apparaît
dans la publication de von Koch de 1904.
Le réel transformé
De manière imagée, l’un des apports décisifs de Mandelbrot a été de prendre le flocon de von Koch pour un véritable flocon. Autrement dit, loin de réduire ce genre de curiosités à de simples cas d’école de courbes ou de surfaces aux propriétés mathématiques exotiques, Mandelbrot a compris que celles-ci pourraient constituer une description nouvelle et puissante de vastes domaines du monde réel.
Comparaison n’est pas raison, mais on peut peut-être risquer une analogie avec la révolution de l’héliocentrisme au XVIIe siècle : alors que les idées de Copernic sur le mouvement de la Terre autour du Soleil étaient demeurées cantonnées aux cercles érudits, la révolution intellectuelle qu’elle annonçait ne s’est véritablement produite que lorsque Galilée, quelques décennies plus tard, a donné à ces réflexions théoriques une résonance concrète.

Flocons de neige et de givre sur une vitre gelée.
Quelques décennies, c’est aussi le temps qu’il faut pour que Mandelbrot donne une nouvelle jeunesse aux travaux tels que ceux de Pierre Fatou et Gaston Julia. Ceux-ci avaient construit des exemples importants d’ensembles fractals (relevant de ce qu’on appelle aujourd’hui la dynamique holomorphe), mais demeurés purement abstraits. On ne trouve que très peu de dessins dans l’imposant mémoire de deux cents pages de Julia sur « l’itération des fractions rationnelles », et ceux-ci ne vont pas plus loin que quelques figures vaguement circulaires incluses les unes dans les autres.
Mandelbrot, lui, dispose des ordinateurs de la firme ibm. Dans les années soixante l’informatique est encore dans l’enfance, mais le type de travail à mener pour prolonger les recherches des précurseurs est parfaitement en ligne avec ce que permet déjà la « stupidité à grande vitesse des ordinateurs », pour reprendre l’expression de James Gleick, le premier à avoir retracé l’histoire de la théorie du chaos en 1987.
Se révèlent ainsi des figures d’un type entièrement nouveau, dont les mots du vocabulaire courant s’avèrent étrangement impuissants à rendre compte : brisures, cassures, irrégularités… Mais l’étrangeté de ces limites langagière est surtout rétrospective, à présent que le regard d’un Mandelbrot a permis de percevoir que les objets fractals ont en réalité toujours été parmi nous, de la forme des nuages à la fréquence des tremblements de terre en passant par l’évolution des cours d’une action cotée en bourse. Aujourd’hui il nous est facile de remarquer qu’un chou romanesco a tout d’un ensemble de choux plus petits eux-mêmes composées de choux toujours plus petits, en une structure fondamentalement similaire à celle du flocon de von Koch. S’il nous semble aussi étrange qu’une telle observation ait dû attendre si longtemps avant d’être faite et étudiée, c’est bien qu’une révolution s’est produite, c’est-à-dire un événement après lequel les choses ne peuvent plus être vues comme avant.
Mandelbrot et la nature : formes et processus
Avant Mandelbrot, le lien entre nature et mathématiques a été abordé par le mathématicien et biologiste écossais D’Arcy Thompson (1860-1948) dans son maître-ouvrage On Growth and Form (« Forme et croissance », 1917, révisé en 1942). Dans la préface, D’Arcy Thompson écrit : « Mon livre a à peine besoin d’une préface, pour la raison qu’il est tout entier une préface, du début à la fin. » Mandelbrot ne manque pas d’y faire écho dans The Fractal Geometry of Nature (« La géométrie fractale de la nature », 1982) en écrivant : « En écho à D’Arcy Thompson, cet essai est une préface du début à la fin. Tout spécialiste qui espère plus sera déçu. »
La référence n’est pas un simple clin d’œil mais bien d’ordre méthodologique. D’Arcy Thompson s’intéresse, comme le biologiste qu’il est, à ce que l’on appellerait aujourd’hui la morphogenèse. Il établit, de façon intuitive et souvent descriptive, des ponts entre les formes du vivant et celles des phénomènes physiques naturels. Point de vue assez éloigné des méthodes modernes, qui s’appuient soit sur la génétique, soit sur les interactions physico-chimiques qui agissent sur l’embryon. Mais la diversité des analogies que D’Arcy Thompson recherche (de nature mathématique, comme dans la structure fibonaccienne de certaines spirales en botanique, de nature mécanique ou encore hydrodynamique) lui interdit un discours dogmatique, de même que les informaticiens d’aujourd’hui seraient bien en peine de définir la notion d’algorithme analogique. Et de même que Mandelbrot, qui avertit : si vous voulez savoir de quoi je parle, regardez les illustrations !
Le fait que Mandelbrot éparpille la définition des fractales tout au long de son livre The Fractal Geometry of Nature reflète sa volonté de lui éviter le statut d’objet formel (certains mauvais esprits diraient : son impuissance à le lui attribuer). Pour lui, une fractale se caractérise avant tout par sa propriété d’invariance par changement d’échelle, une propriété foncièrement visuelle et conséquence d’un processus itératif.
Les fractales nous font ainsi pénétrer dans le monde des dynamiques créatives.
La notion de système dynamique est entrée vigoureusement dans le monde de la physique et des mathématiques à la fin du XIXe siècle. Paradoxalement, Henri Poincaré en est l’une des figures majeures, lui qui n’était pas tendre pour les objets « pathologiques » qui fourniront aux fractales leurs plus beaux exemples.
Bernard Randé

références
•
La Théorie du chaos – Vers une nouvelle science. James J. Gleick,
Flammarion, 1987.
• Mémoire sur l’itération des fonctions rationnelles. Gaston Julia,
Journal de mathématiques pures et appliquées, 8e série, tome 1, 1918.
•
Sur une courbe continue sans tangente obtenue par une construction géométrique élémentaire. Helge von Koch, Arkiv för matematik, astronomi och fysik vol. 1, 1904.


