
D’étranges panneaux étaient accrochés à l’entrée de certains temples bouddhistes ou shintoïstes au Japon, durant la période d’Edo (1603‒1867). On pouvait en effet y trouver une énigme géométrique à résoudre. Ce sont les fameux sangaku (littéralement, « tablettes mathématiques »). Quelque neuf cent sangaku nous sont parvenus ou sont documentées.
Le problème géométrique posé représente souvent un véritable défi, non par les connaissances requises, mais par la complexité des solutions, qui parfois s’étendent sur plusieurs pages !
L’aspect esthétique n’est jamais négligé : des couleurs sont utilisées et les figures gravées, d’une manière générale, respectent un sens exquis de l’harmonie ou de l’égance. L’idée de tangence est omniprésente dans les sangaku.
Peu de connaissances requises
Ce qui fascine les mathématiciens amateurs (et professionnels) dans les sangaku, c’est le peu de connaissances requises : le théorème de Pythagore est un incontournable, les cas de similitude des triangles également. La loi des sinus (voir encadré), le calcul des aires, la résolution des équations de degré 2, la notion d’inversion par rapport à un cercle sont également utiles. Il est cependant difficile de savoir comment ces notions étaient appréhendées par les mathématiciens japonais de l’époque.
La difficulté est ailleurs : résoudre un « problème sangaku » nécessite beaucoup de patience, de l’imagination, et un certain entraînement.
La loi des sinus
La figure ci-dessous met en présence un triangle ABC inscrit dans un cercle. On a noté a = BC, b = AC et c = AB. Par construction, l’angle est droit, donc
où D désigne le diamètre du cercle. Mais
et
sont des angles égaux (car ils sont inscrits dans le cercle et interceptent la même corde [BC]). Donc, en posant
on a
. Si l’angle
est obtus, on raisonne de même en remarquant que
(on confond ici un angle et sa mesure).
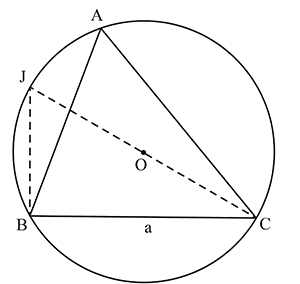
Avec des notations évidentes, on a de même ; c’est la loi des sinus.
Nombre de problèmes font intervenir des cercles tangents et des droites tangentes aux cercles, sans que la définition de la tangence soit explicitée. Par exemple, on donne une figure et il s’agit de trouver une relation entre les rayons des cercles considérés.
Voici quelques exemples. Dans la suite, chaque cercle (Ci ) aura pour centre Oi et pour rayon ri. Les solutions sont données dans le dernier encadré de l’article. Le lecteur est invité à les chercher avant !
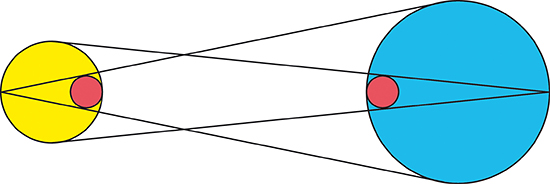
Sur la figure ci-dessus, on se donne les tangentes aux deux grands cercles (C1) et (C2). On constate qu’il existe deux petits cercles (C’1) et (C’2) tangents respectivement à deux droites et à un grand cercle. On ne précise pas comment sont construits ces deux petits cercles, mais on observe qu’ils ont apparemment des rayons égaux : c’est ce qu’il faut prouver.
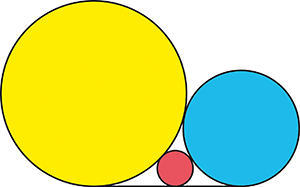
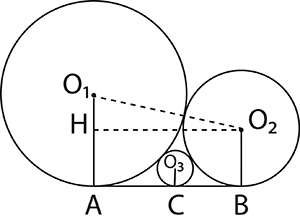
Sur la figure ci-contre, trois cercles tangents deux à deux sont considérés ; ils sont tous les trois tangents à une droite. La relation entre les trois rayons des cercles n’est pas évidente, mais le point important est de deviner qu’il existe bien une relation.
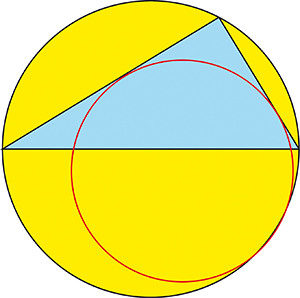
Sur la figure suivante, le cercle (C2) est tangent à deux côtés du triangle rectangle et au cercle (C1). Ce dernier est circonscrit au triangle dont l’hypoténuse est un diamètre. On ne précise pas comment est construit (C2). Il s’agit de démontrer que r2 = a + b ‒ c (où c est la longueur de l’hypoténuse du triangle, a et b étant les longueurs des deux autres côtés).
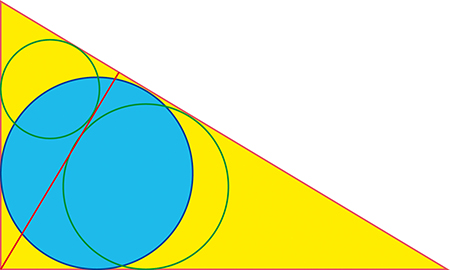
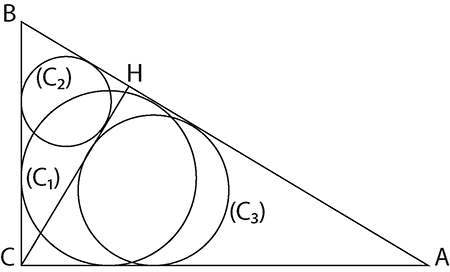
Dans le triangle rectangle de cette dernière figure, la droite qui sépare le triangle en deux est perpendiculaire à l’hypoténuse. Il convient de montrer que la longueur de cette perpendiculaire est égale à la somme des rayons des trois cercles.
Des énigmes pour l’historien
Au-delà des problèmes mathématiques qu’ils représentent, les sangaku constituent autant d’énigmes historiques.
Pourquoi, subitement, au début du XVIIe siècle, les samouraïs puis les amateurs de mathématiques, au Japon, ont-ils étudié ces problèmes parfois redoutables ? Les sangaku semblent ne pas avoir d’applications pratiques ; dès lors, quelles sont leurs origines possibles ? D’où proviennent les méthodes de démonstrations utilisées par les mathématiciens japonais ? Quelles ont été les influences éventuelles des mathématiques grecques ; sont-ce par exemple les Éléments d’Euclide, qui furent traduits en chinois et publiés à Pékin en 1607 ? Les Japonais avaient des relations culturelles avec leur grand voisin et les lettrés japonais lisaient le chinois. Aucune preuve, actuellement, ne peut être fournie sur l’influence d’Euclide sur les mathématiques japonaises ; inversement, on ne peut pas exclure que l’œuvre d’Euclide ait été connue.
On peut aussi rechercher des liens entre la création de sangaku et les pratiques religieuses, ou encore avec l’art japonais du XVIIe siècle…

Les solutions des énigmes
Premier sangaku : Les cercles (C2) et (C’1) sont inscrits dans le même secteur de sommet A. Ils vérifient donc r2 / r’1 = AD / AB. De même pour (C1) et (C’2) dans le secteur de sommet D. On en déduit : r1 / r’2 = DA / DC.
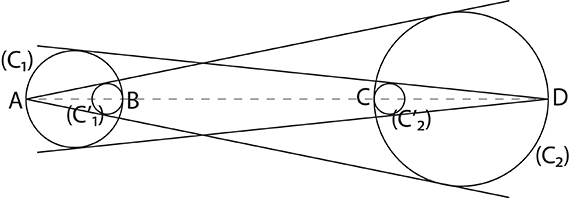
Cela nous donne AB × r2 × r’2 = DC × r1 × r’1, c’est-à-dire 2r1 r2 r’2 = 2r2 r1 r’1. On en conclut bien que r’1 = r’2.
Deuxième sangaku : En utilisant le théorème de Pythagore dans le triangle O1O2H, on montre que AB est égal à : en effet, on a AB2 + (r1 ‒ r2)2 = (r1 + r2)2, c’est à dire AB2 = 4r1r2 en simplifiant.
En utilisant le même procédé pour les cercles (C1) et (C3), on obtient , puis
avec les cercles (C2) et (C3).
Comme AB = AC + BC, on en déduit facilement que
Troisième sangaku : Dans le triangle ABC, on note classiquement a (respectivement b, c) la longueur du côté opposé au sommet A (respectivement B, C).
Dans le triangle rectangle O1O2H, on a O1O2 = c / 2 ‒ r2, puis O1H = b / 2 ‒ r2 et enfin O2H = a / 2 ‒ r2. On en déduit l’égalité suivante :
(b / 2 ‒ r2)2 + (a / 2 ‒ r2)2 = (c / 2 ‒ r2)2. En développant et en remarquant que c2 = a2 + b2, on en déduit que r2 = a + b ‒ c.
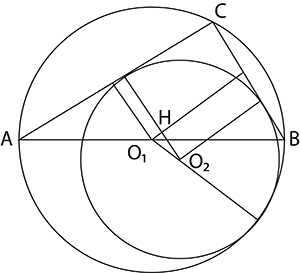
Quatrième sangaku : Dans le triangle rectangle ABC, le rayon du cercle inscrit (C1) est donné en fonction de la longueur des côtés par 2r1 = a + b ‒ c (voir en page 6). De la même manière, 2r2 = HB + HC ‒ a et 2r3 = HA + HC ‒ b.
En sommant les trois égalités, on obtient 2(r1 + r2 + r3) = HB + HA ‒ c + 2HC, ce qui se simplifie en HC = r1 + r2 + r3 puisque c = HA + HB.
références
• Sangaku. Le mystère des énigmes géométriques. Géry Huvent, Dunod, 2008. • Sacred Mathematics, Japanese Temple Geometry. Fukagawa Hidetoshi et Tony Rothman, Princeton University Press, 2008. • Les mathématiques japonaises à l’époque d’Edo. Annick Horiuchi, Vrin, 1994.


