On trouve des traces des carrés magiques en Inde ou en Chine bien avant l’ère chrétienne. Dans ces tableaux remplis d’entiers consécutifs, la somme des nombres alignés horizontalement, verticalement ou dans les deux diagonales est identique. Les Chinois surnommèrent Lo-Shu le carré mythique ci-contre, d’après la légende qui veut que, pour calmer la colère du fleuve Lo, les prêtres durent faire quinze sacrifices, 15 étant la constante du carré magique représenté sur le dos d’une tortue sortant du fleuve en crue. Les carrés magiques auraient été introduits en Europe par Emanuel Moschopulos, un auteur byzantin qui vécut à Constantinople au début du XVe siècle.
 Les carrés magiques ont fait l’objet d’un dossier dans Tangente 161 (2014). Une variante arithmétique mérite d’être explorée plus avant : les carrés magiques constitués uniquement de nombres premiers consécutifs. Le mathématicien américain Harry Lewis Nelson (né en 1932) a construit le carré magique 3 × 3 suivant, contenant les plus petits nombres premiers consécutifs. C’est un exploit énorme !
Les carrés magiques ont fait l’objet d’un dossier dans Tangente 161 (2014). Une variante arithmétique mérite d’être explorée plus avant : les carrés magiques constitués uniquement de nombres premiers consécutifs. Le mathématicien américain Harry Lewis Nelson (né en 1932) a construit le carré magique 3 × 3 suivant, contenant les plus petits nombres premiers consécutifs. C’est un exploit énorme !
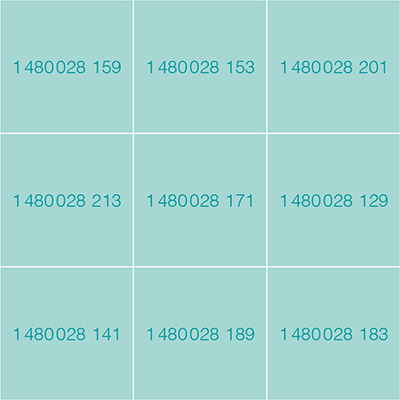
Il existe en fait un nombre infini de carrés magiques 3 × 3 composés uniquement de nombres premiers consécutifs ; en voici un autre.
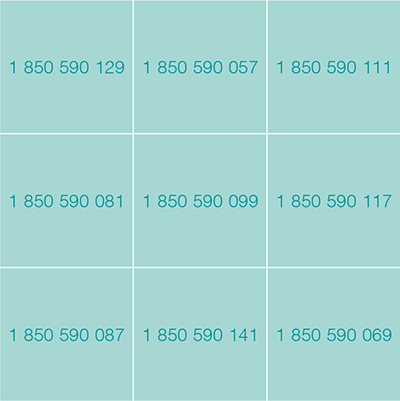
De manière peut-être surprenante, les carrés magiques d’ordre 5 composés de nombres premiers consécutifs sont plus faciles à réaliser.
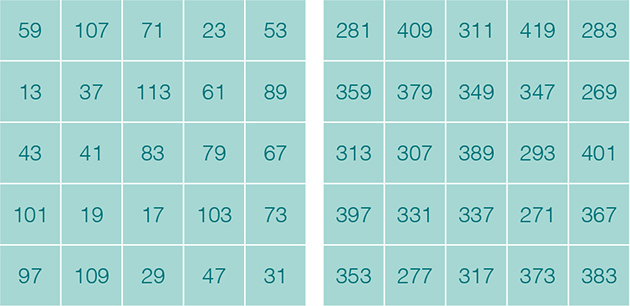
Encore plus étonnants sont les carrés magiques composés de nombres premiers (non consécutifs) qui restent premiers si l’on ajoute à chaque entier un nombre N. Expérimentons ce phénomène avec le carré magique d’ordre 4 ci-dessous créé par le mathématicien Allan William Johnson Jr.
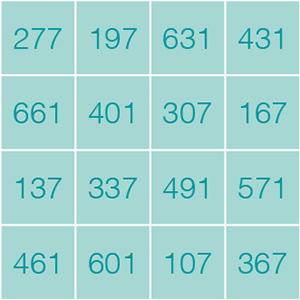
Ajoutons donc 30 aux nombres dans chaque case et nous obtenons à nouveau un carré magique de nombres premiers :
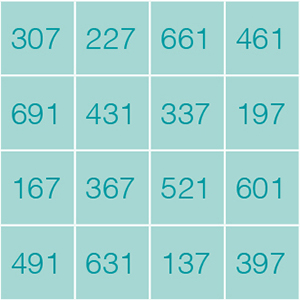
Pour conclure, ajoutons maintenant 1 092 aux nombres dans chaque case. On obtient encore une fois un carré magique de nombres premiers à quatre chiffres !
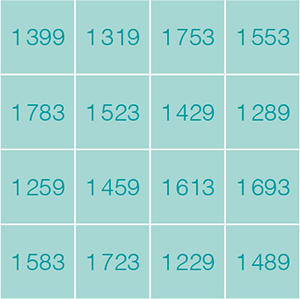
Époustouflant, non ? Et maintenant, à vous de prendre le relai et d’épater vos amis avec vos propres carrés magiques premiers !

