Le dessin d’un triangle ABC vous est proposé sur une feuille de papier. Comment obtenir ABC d’un seul coup de ciseaux rectiligne dans la feuille ? Avec trois coups de ciseaux, c’est facile : on coupe le long de [AB], puis le long de [BC], et enfin le long de [CA]. Mais avec un seul coup de ciseaux ?
Vous savez construire avec un compas la bissectrice de ses angles. Vous savez en outre que les trois bissectrices intérieures (AO), (BO) et (CO) se coupent en O, le centre du cercle inscrit. Ce cercle est tangent aux trois côtés du triangle.
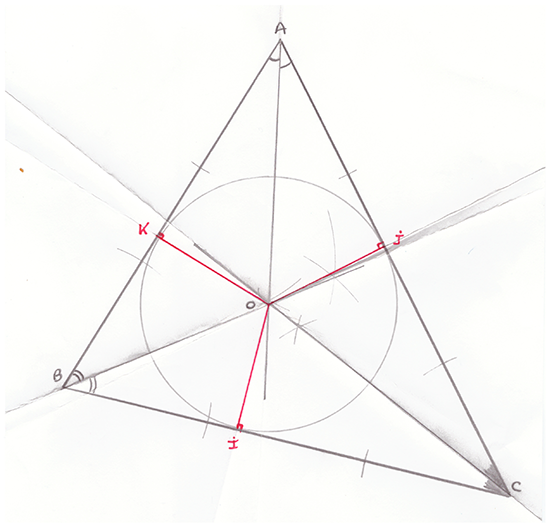
Abaissons depuis O les perpendiculaires (OI), (OJ) et (OK) aux trois côtés de ABC. Les trois distances du point O aux côtés du triangle sont égales : OI = OJ = OK.
Maintenant, il s’agit de plier la feuille de papier. Marquons trois plis de la feuille selon les bissectrices (AO), (BO) et (CO) en plis montagnes. Marquons ensuite trois plis vallées (en creux) selon (OI), (OJ) et (OK). Plions en deux la feuille selon la bissectrice (AO) en pli montagne : par transparence de la feuille, on peut voir les droites (AB) et (AC) se superposer, même si les longueurs AB et AC ne sont pas égales.
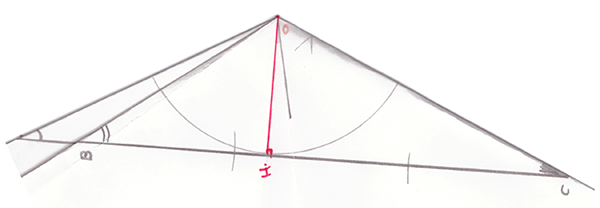
En tenant la feuille avec le point O vers le haut, utiliser les trois plis vallées pour que les segments [OI], [OJ] et [OK] soient confondus et verticaux. En regardant au-dessus du point O, on voit trois plans se coupant selon la verticale issue de O passant par notre œil. Si l’on rabat l’un des trois plans sur l’un des deux autres, on voit des superpositions de droites. Par exemple, (BIO) peut se superposer sur (AKO), et la droite (BI), donc (BC), se superpose à la droite (AK), donc à (AB). De même, (BKO) peut se superposer sur (CIO), et la droite (BK), donc (BA), se superpose à la droite (CI), donc à (CA). Enfin, les droites (AB), (BC) et (AC) peuvent se superposer (à voir par transparence).

Les maths, c’est magique !
Vous pouvez couper d’un seul coup de ciseaux en ligne droite selon le plus grand côté (le segment [AC] ici). Du même coup, vous couperez les deux autres côtés superposés. Vous pouvez aussi replier les trois plans l’un sur l’autre pour faire votre opération (sur une épaisseur plus grande) : la découpe rectiligne sera plus courte, et dégagera encore le triangle.
Une petite vidéo de ce découpage est disponible en ligne dans le cadre des « Capsules de Fermat » (La Découpe d’un triangle d’un seul coup, 5 min 35 s, Fermat Science, 2022)
En utilisant les mêmes propriétés géométriques que pour le triangle ABC, saurez-vous généraliser cette découpe à d’autres polygones ? Lesquels ? En quoi la connaissance du cercle inscrit dans ce polygone est-elle utile ?

