Le premier à s’être intéressé aux « bases de numération négatives » est le mathématicien italien Vittorio Grünwald. Il fournit dans Giornale di Matematiche di Battaglini (1885) des algorithmes pour effectuer les opérations arithmétiques usuelles. Elles ont ensuite été redécouvertes en 1936 par le mathématicien britannico-américain Aubrey Kempner, puis en 1959 par les mathématiciens polonais Zdzis?aw Pawlak et Andrzej Wakulicz. Ces derniers ont notamment implanté un système utilisant la base négabinaire (base – 2) sur les premiers ordinateurs conçus en Pologne à la fin des années 1950. L’intérêt de cette base était qu’elle supprimait le bit de signe, mais les opérations arithmétiques étant plus compliquées à mettre en œuvre, ces essais n’ont pas eu de descendance.

Dans le système négabinaire, un entier N se décompose en puissances de – 2 :
N = a1 × (– 2)0 + a2 × (– 2)1 + a3 × (– 2)2 + a4 × (– 2)3 + … où les bits ai valent tous 0 ou 1. Un tableau de conversion des entiers de – 5 à 5 peut être dressé.

Les nombres strictement négatifs s’écrivent tous avec un nombre pair de chiffres ; les nombres positifs s’écrivent eux avec un nombre impair de chiffres. Seuls les nombres positifs égaux à une somme de puissances de 2 distinctes et d’exposants tous pairs, comme 0, 1, 4, 5, 16, 17, 20, 21, ont la même écriture en binaire et en négabinaire. On obtient les opposés de ces nombres strictement positifs en ajoutant simplement un 1 devant l’écriture négabinaire du nombre positif : – 22n = – 22n+1 + 22n.
Pour convertir un nombre N écrit en base 10 en négabinaire, la méthode est la même que pour la conversion en base 2 : on divise successivement N par – 2 et on considère les restes successifs pris dans l’ordre inverse de leur obtention. La seule difficulté est que le reste doit être égal à 0 ou + 1. Par exemple, la division de – 127 par – 2 donnera 64 avec pour reste + 1, et non 63 (qui correspondrait à un reste égal à – 1). Pour les entiers positifs, il est aisé de convertir directement l’écriture binaire en négabinaire. Prenons l’exemple de 235, qui s’écrit 11101011 en binaire.
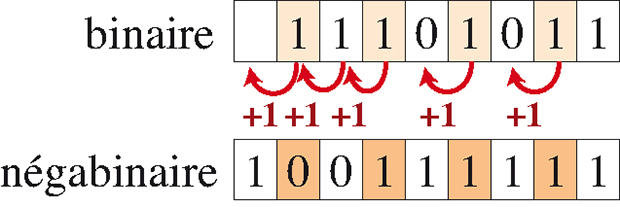
On vérifie que 235 = 28 – 25 + 24 – 23 + 22 – 21 + 20. En partant de la droite dans l’écriture binaire, toutes les cases de rang pair contenant 1 donnent lieu à l’ajout de 1 dans la case située immédiatement à gauche, avec retenue et report éventuel si la case située immédiatement à gauche contient déjà un 1.
Pour obtenir l’écriture négabinaire de l’opposé d’un nombre strictement positif, on procède comme suit.
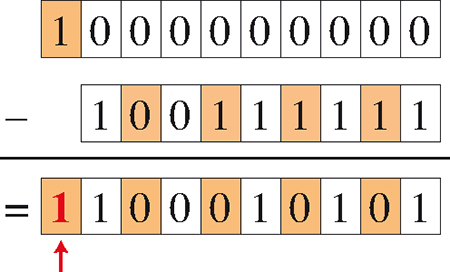
On soustrait l’écriture négabinaire du nombre positif du nombre 100…00 ayant un chiffre de plus et constitué d’un seul chiffre 1 suivi de zéros, puis on ajoute un 1 devant l’écriture du résultat. On vérifie que –235 = –29 + 28 + 24 + 22 + 20.
Écrivez 2 019 en binaire, puis convertissez-le en négabinaire.
La base négaternaire fonctionne de la même façon avec les puissances successives de – 3.
Ecrivez 2 019 en base ternaire, puis convertissez-le en négaternaire.

