Comment montrer qu’une somme de huit nombres entiers dont le plus grand est 5 peut s’écrire comme la somme de cinq nombres entiers dont le plus grand est 8 ? Le petit diagramme suggère une méthode, qui est toujours réalisable. En faisant pivoter le dessin de gauche (qui illustre la somme 1 + 2 + 3 + 3 + 3 + 4 + 4 + 5) d’un quart de tour dans le sens de la flèche, on a transformé la somme de huit nombres rangés dans l’ordre croissant en une somme de cinq nombres (8 + 7 + 6 + 3 + 1) rangés dans l’ordre décroissant.
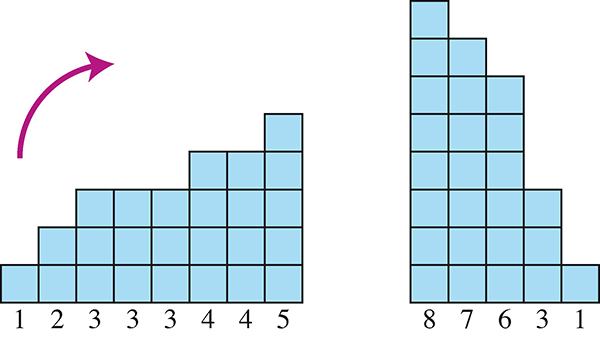
Le nombre de « cases unités » étant conservé, on a évidemment l’égalité
1 + 2 + 3 + 3 + 3 + 4 + 4 + 5 = 1 + 3 + 6 + 7 + 8 = 25.
On obtient donc deux partitions (écritures à base de somme d’entiers non nuls) du nombre 25, qui sont duales l’une de l’autre. Ce type de diagramme est appelé diagramme de Ferrers (nommé ainsi d’après le mathématicien britannique Norman Ferrers). Alors qu’il était étudiant et qu’on lui posait le problème « Démontrer que le nombre de partitions d’un entier en n parties est égal au nombre de partitions de cet entier dont la plus grande partie est n », Ferrers le résolut très facilement à l’aide d’un tel diagramme.
La propriété illustrée ci-dessus est bien sûr généralisable à une somme quelconque de n nombres entiers strictement positifs (où n > 0) dont le plus grand est p (avec p > 0). On peut avoir p = n et, dans ce cas, les deux sommes peuvent être soit différentes, soit identiques. Lorsque les deux diagrammes sont identiques, la partition qu’ils représentent est dite auto-duale.
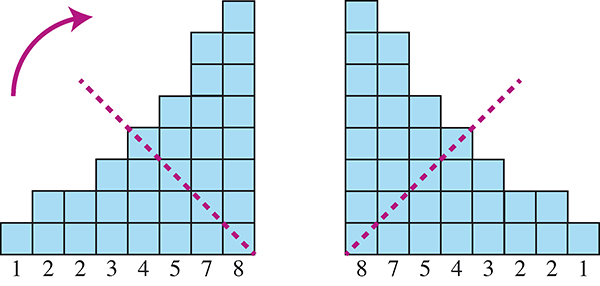
Partition auto-duale du nombre 32.
Un théorème d’Euler énonce que le nombre de partitions de l’entier n en parts impaires et distinctes est égal au nombre partitions de n auto-duales.
1. Trouvez toutes les partitions auto-duales du nombre 10.
Maxi des mini ou mini des maxi ?
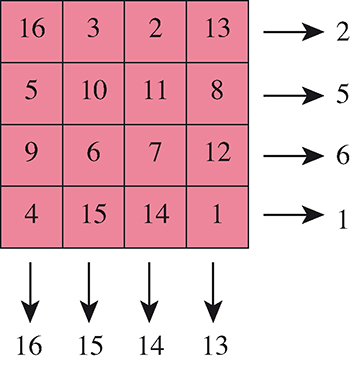
À partir de ce tableau de nombres tous différents (il s’agit du fameux carré magique de Dürer, mais ce pourrait être un carré quelconque), on a écrit à gauche les minima de chaque ligne, et en bas les maxima de chaque colonne. Or, dans tout tableau rectangulaire de nombres tous différents, le minimum des maxima des colonnes est toujours supérieur ou égal au maximum des minima des lignes.
2. Mais peut-on avoir égalité ? Dans quels cas ?

