Une fois n’est pas coutume, Bêta promène le long des couloirs de l’Institut intergalactique un air quelque peu perturbé.
« Que t’arrive-t-il ? lui demande sa camarade Epsilon, prompte à s’inquiéter du bien-être de son prochain.
– J’ai surpris une étrange conversation entre les professeurs Phi, Sigma et Omicron, lui répond le jeune homme. Ça a commencé par le professeur Phi qui disait : “Je ne sais pas quels sont les nombres X et Y.” Ce à quoi Sigma a répondu : “Je le savais.” Et là, Phi a dit : “Je connais maintenant les valeurs de X et Y.” Et tu sais ce que Sigma a déclaré ? “Moi aussi.” Alors Omicron a ajouté : “Moi de même !” Puis ils sont partis tous les trois du rire démoniaque qui caractérise les professeurs de l’Institut intergalactique. Quand j’ai osé demander au professeur Omicron la signification de tout ceci, il m’a simplement précisé : “Ce que nous savions tous les trois, c’était que X et Y étaient deux nombres entiers tels que 1 < X < Y et X + Y ≤ 100. Avant leur discussion, Phi connaissait la valeur du produit XY et Sigma celle de la somme X + Y. Et moi, rien du tout.” Sur ce, ils sont partis ensemble en gloussant comme des pingouins.
– Ça glousse, les pingouins ? s’interroge Epsilon avant d’ajouter : En tout cas, je peux te dire que les valeurs de X et Y sont 4 et 13. »
Bêta fronce les sourcils :
« Tu fais partie de la même secte, avoue !
– La secte de ceux qui ont quelques connaissances en mathémagie, se moque gentiment Epsilon. J’avais déjà entendu parler de cet échange que l’on appelle problème de Freudenthal, et je me souvenais de sa solution unique. La résolution est simple sur le principe, quoiqu’un peu fastidieuse. »
Le problème impossible
Epsilon déroule le raisonnement qui conduit à la solution du problème de Freudenthal, dit aussi problème impossible. Mettons-nous à la place d’Omicron pour raisonner. Si Phi ne peut pas déduire X et Y de la connaissance de leur produit, cela signifie que ce produit est ambigu : il y a au moins deux décompositions qui permettent de l’obtenir. Avec les contraintes données par Omicron, cette table des produits ambigus TPA comporte 574 éléments et commence par {12, 18, 20, 24, 28, 30…}. Le produit XY est un élément de cet ensemble.
Quand le professeur Sigma précise qu’il savait que Phi ne pouvait pas connaître X et Y, cela signifie que la somme dont il est en possession ne peut se décomposer qu’en X+Y tels que XY appartiennent à TPA. Après une analyse qui peut être systématique mais assez longue, on arrive à une « table des sommes possibles » TSP qui ne contient cette fois plus que dix éléments : 11, 17, 23, 27, 29, 35, 37, 41, 47 et 53.
Cette connaissance est à présent disponible pour Omicron et Phi, et il se trouve qu’elle permet à ce dernier de conclure concernant les valeurs de X et Y : cela implique que le produit en sa possession n’apparaît qu’une fois dans le tableau formé par l’ensemble des produits possibles liés à chaque somme possible. Par exemple, avec 11 = 2 + 9 = 3 + 8 = 4 + 7 = 5 + 6, ces produits sont 18, 24, 28 et 30. Avec
17 = 2 + 15 = 3 + 14 = 4 + 13 = 5 + 12 = 6 + 11 = 7 + 10 = 8 + 9,
ces produits sont 30, 42, 52, 60, 66, 70 et 72. On voit déjà que 30, que l’on retrouve deux fois, ne convient pas.
Omicron et Sigma font la même chose pour les autres sommes de TSP et éliminent les produits qui apparaissent plusieurs fois. Or, cela permet à Sigma de déterminer X et Y. Cela n’est possible que si la somme qu’elle connaît impose un produit unique. En faisant les calculs, on trouve que la seule valeur de somme qui conduit à une valeur de produit unique est 17, le produit correspondant étant 52. Ces informations sont maintenant en possession d’Omicron, qui peut conclure.
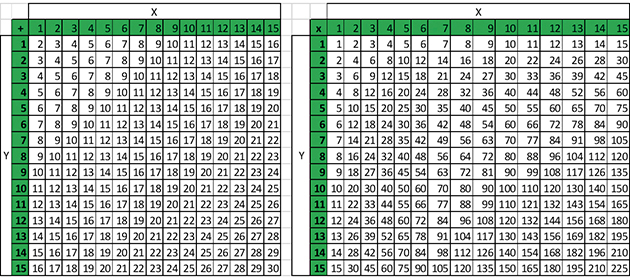
« Normalement, je t’aurais arrêtée au début de tes explications, commente Bêta, mais j’exploiterais bien cette histoire pour proposer un article sous forme d’énigme au magazine Cosinus qui a été lancé par le professeur Phi. Je suis sûr que ça m’aidera à marquer des points avec lui ! Je vais juste simplifier un peu le problème en remplaçant la condition X + Y ≤ 100 par X et Y inférieurs à 15, ça colle avec les solutions X = 4 et Y = 13. Et je fournirai les tables d’addition et de multiplication associées pour que les lecteurs n’aient pas trop de calculs à faire. »
Chers lecteurs, que pensez-vous de l’idée de Bêta ?

