Entrez dans la danse

Dans ce club de danse, on pratique toutes sortes de danses : des danses modernes, des danses traditionnelles (bourrées du Berry, du Morvan ou d’Auvergne, gavottes de Bretagne, sauts du Pays basque, rondes à trois pas de Normandie…), des danses par paires, des danses et contredanses en ligne, des danses en cortège, des danses en quadrettes (avant-deux de travers), et des danses en cercle ou en chaîne. Le club compte vingt membres constitués de dix couples* à la ville : dix hommes et dix femmes.

Danses en couple

Pour éviter que chaque membre du club ne danse toujours avec son conjoint, les animateurs font tirer au sort les cavalières pour les attribuer à un cavalier.

Quelle est la probabilité qu’aucune personne ne danse avec son conjoint ?

Ce problème est de même nature qu’une question posée par Pierre Rémond de Montmort (1678–1719) et étudiée par le grand mathématicien suisse Leonhard Euler (1707–1783), qui publia en 1753 un mémoire de quinze pages sur ce problème dit des rencontres.

Le jeu de rencontre est un jeu de hasard où deux personnes, ayant chacune un entier jeu de cartes, en tirent à la fois une carte après l’autre, jusqu’à ce qu’il arrive qu’elles rencontrent la même carte ; et alors une des deux personnes gagne. Or, lorsqu’une telle rencontre n’arrive point du tout, alors c’est l’autre des deux personnes qui gagne.

Revenons à nos danseurs. Si n désigne le nombre de couples numérotés de 1 à n, le tirage au sort donnera la suite des numéros des femmes dansant respectivement avec les hommes numérotés de 1 à n. Il y a donc en tout n! cas possibles. Pour n = 10, le nombre de paires possibles est égal à 10!, soit 3 628 800.

Le principe du calcul : il y a alors dix partenaires potentielles pour le premier danseur, il n’en reste plus que neuf pour le deuxième, et ainsi de suite…

À l’intersection de la ligne L et de la colonne n, le tableau suivant indique, pour n paires de danseurs (1 ≤ n ≤ 10), le nombre d’occurrences où le premier couple formé d’une danseuse appariée avec son conjoint porte le numéro L.

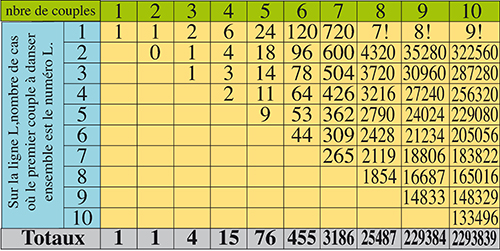
La ligne 1 du tableau indique, pour chaque valeur de n, le nombre K (n, 1) de cas où le couple 1 danse ensemble.

On constate, bien entendu, que c’est le nombre de suites possibles des n – 1 nombres restants, compris de 2 à n, soit (n – 1)! cas. On remplit ainsi la ligne 1.

Plus généralement, la ligne k contiendra les nombres K (n, k) de suites où k est le premier couple appelé à danser ensemble.

Supposons maintenant que le tirage ne fasse pas danser ensemble les couples de 1 à p, mais que ce soit le cas du couple p + 1. Comment calculer le nombre de situations ?

Euler a eu l’idée géniale : supprimer le couple p + 1 de la liste ! Il faut donc retirer des
(n – 1)! suites de n – 1 nombres celles où l’une des p premières paires est un couple. Ainsi :

K (n, p + 1) = (n – 1)! – K (n – 1, 1) – K (n – 1, 2) –… – K (n – 1, p).

Pour p = 1, cela donne :

K (n, 2) = (n – 1)! – K (n – 1, 1) = (n – 1)! – (n – 2)! = K (n, 1) – K (n – 1, 1),

d’où la deuxième ligne.

Pour p = 2 :

K (n, 3) = (n – 1)! – K (n – 1, 1) – K(n – 1, 2) = K (n – 1, 1) – K (n – 1, 2)…

De proche en proche, on arrive à :

K (n, p + 1) = K (n – 1, p + 1) – K (n – 1, p).

On en déduit la construction du tableau, dans lequel chaque terme est égal à la différence des deux termes de la ligne précédente, situés dans la même colonne et dans la colonne précédente.

Mais on peut aussi dire que :

K (n, 1) = (n – 1)!,

K (n, 2) = (n – 1)! – (n – 2)!,

K (n, 3) = [(n – 1)! – (n – 2)!] – [(n – 2)! – (n – 3)!] = (n – 1)! – 2(n – 2)! + (n – 3)!,

K (n, 3) = (n – 1)! – 3(n – 2)! + 3(n – 3)! – (n – 4)!

Et ainsi de suite… On reconnaît les coefficients du triangle de Pascal, avec un signe alterné.

Compte tenu de la façon d’obtenir ces coefficients, la somme de ces valeurs associe également à chaque factorielle un coefficient de ce triangle (avec un signe alterné).

Dans le cas n = 10, cela donne :

K (10, 1) +… + K (10, 10) = 2 293 839
= 10 × 9! – 45 × 8! + 120 × 7! – 210 × 6! + 252 × 5! – 210 × 4! + 120 × 3! – 45 × 2! + 10 × 1! – 1 × 0!

En divisant par 10!, on obtient la probabilité qu’au moins une paire de danseurs soit constituée de deux conjoints :

On en déduit la probabilité qu’aucun membre du club ne danse avec son conjoint, égale à :

soit environ 0,36787946.

Lorsque le nombre de danseurs tend vers l’infini, cette probabilité tend vers 1/e, soit environ 0,36787944117.

Des danses en ligne

Supposons maintenant que pour une danse, dix danseurs se placent en ligne de façon totalement aléatoire, sans tenir compte du sexe. Ils effectuent une première danse (kost ar c’hoad), puis pour une seconde danse en ligne (un laridé), ils se replacent de façon aléatoire.

1. Quelle est la probabilité que personne ne se retrouve avec les mêmes voisins que lors de la première danse en ligne ?

Une piste : le problème équivaut à réarranger les nombres de 1 à 10 de telle sorte que la différence entre deux nombres voisins (en valeur absolue) soit toujours strictement supérieure à 1.

À vous de jouer ! Danses en cercle

Le club initie aussi ses adhérents à des danses traditionnelles, dont certaines se dansent en cercle ou en ronde. Ici encore, on supposera que les danseurs se placent aléatoirement, indépendamment du sexe.

Les danseurs effectuent une première danse (un branle de Lorraine), puis une seconde (une brande), en se réarrangeant de façon aléatoire.

2. Quelle est la probabilité que personne ne se retrouve avec les mêmes voisins que lors de la première danse en cercle ?

3. Reprendre les questions 1 et 2 avec la contrainte d’une alternance des hommes et des femmes (comme pour un cercle circassien ou une bourrée des dindes).

Ce numéro ayant un dossier consacré aux questions ouvertes, vous ne trouverez pas dans ce numéro la réponse aux questions 2 et 3. Nous vous proposons de nous écrire à
courrierdeslecteurs@poleditions.com pour nous donner la vôtre !

* Dans cet article, les couples sont effectivement les couples à la ville ; les paires désignent les duos de danseurs que le hasard ou les affinités a constitués le temps d’un atelier.