
Les ouvrages de la Bibliothèque Tangente sont assimilés à des solides homogènes rigides ayant tous exactement les mêmes dimensions et la même masse. Prenons comme unité de longueur la longueur d’un livre. Avec un seul livre, le surplomb maximal est égal à 1/2.
Insérons un deuxième livre sous le premier, de façon que son extrémité droite arrive bord de la table, puis faisons glisser l’ensemble vers le bord de la table tant qu’il reste en équilibre. On peut faire glisser cet ensemble jusqu’à ce que le surplomb du deuxième livre atteigne 1/4, mais pas au-delà car le centre de gravité de l’ensemble des deux livres se situe aux trois quarts du deuxième livre en partant de la gauche (et aux trois quarts du premier en partant de la droite).
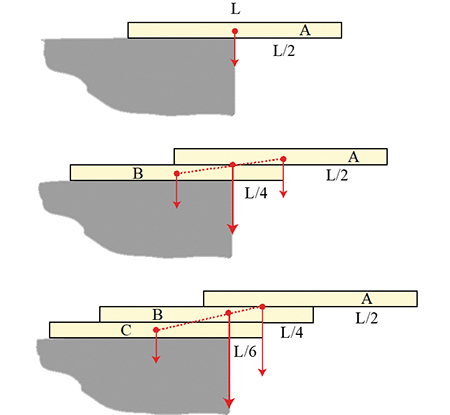
Glissons ensuite un troisième livre sous le deuxième de telle sorte que son extrémité droite arrive au ras de la table, puis faisons glisser l’ensemble vers le bord de la table. L’ensemble restera en équilibre jusqu’à ce que le troisième livre ait un surplomb égal à 1/6.
En continuant de la sorte jusqu’à n livres, le surplomb maximal correspond à la somme 1/2 + 1/4 + 1/6 + 1/8 + 1/10 + … + 1/(2n), soit la moitié de la somme des n premiers termes de la série harmonique. Or, cette dernière diverge : elle peut atteindre une valeur aussi grande que l’on veut (voir Suites et Séries, Bibliothèque Tangente 41, 2011, ou Tangente 182, 2018). Donc, en théorie, on pourrait obtenir un surplomb aussi grand que l’on veut, à condition d’avoir suffisamment de livres.
Une formule d’Euler bien pratique
Lorsque n devient « grand », une valeur approchée de la somme H(n) des n premiers termes de la série harmonique est donnée par une formule due à Euler : H(n) vaut environ ln(n) + γ, où γ est la constante d’Euler-Mascheroni, égale à environ 0,577215.
1. En supposant que vous ayez les soixante-quatorze premiers numéros de la collection Bibliothèque Tangente (courez vite en page 4 pour vous procurer ceux qui vous font défaut !), quel surplomb maximal pourriez-vous obtenir ?
L’empilement de quatre livres par la méthode précédente permet d’atteindre un surplomb égal à 25/24, soit environ 1,0417. On peut faire mieux en utilisant un ou deux livres comme contrepoids.
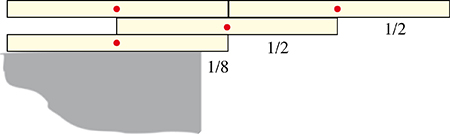
On obtient ici un surplomb égal à 27/24, soit 1,125.
Dans un article de 1979, le mathématicien britannique Stephen Ainley (né en 1952) améliore ce résultat avec la disposition suivante où le surplomb atteint 1/2 + 2/3, soit environ 1,1667.
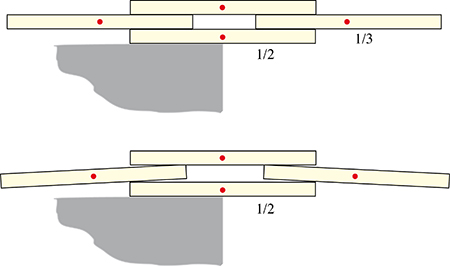
On ne peut pas écarter davantage les deux livres du niveau 2, car les moments des forces en présence soulèvent le livre du niveau 3 et disloquent l’ensemble. Mais Ainley améliora encore un peu ce résultat avec cette disposition non symétrique.
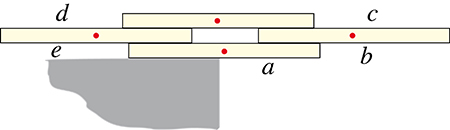
2. Sachant que c = (19 – 10) / 7, d = (31 – 26) / 28 et e = (11 – ) / 14, calculez a + b.

