Voici ce que le mathématicien Georges Papy, véritable « pape » de l’introduction des mathématiques dites « modernes » en Belgique dans les années 1970, proposait comme exercice pratique pour des élèves de niveau collège.
« Dans une classe, chaque élève écrit son nom sur une feuille de papier. On ramasse les “cartes de visites” ainsi obtenues, on les mélange et on les redistribue.
Ensuite, on demande que chaque élève prenne, de sa main droite, la main gauche de celui dont il a la carte de visite. Une personne qui recevrait sa propre carte tiendrait sa propre main gauche avec sa main droite. On obtient ainsi un certain nombre de “rondes”, pouvant éventuellement être réduites à un seul élément.
1. Représentez un exemple d’une telle situation dans un groupe de quinze élèves présentant cinq rondes.
On adoptera la convention suivante :

représente l’élève D possédant la carte de visite a de l’élève A.
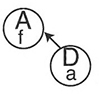
représente l’élève D prenant la main de l’élève A, puisqu’il possède sa carte de visite a.
2. Si n était le nombre de rondes obtenues, que deux élèves quelconques échangent leurs cartes de visite, et que l’on réorganise alors les élèves selon la même règle, quel sera le nombre de rondes après l’échange ? »

