Ce problème et la réponse sont peints sur le temple de Mangan-ji de la préfecture de Fukushima au Japon. Toutes les longueurs seront exprimées en décimètres.
On prend une feuille de papier carrée ABCD de côté 1 dm. On plie la feuille de façon que le coin A se positionne en Q sur le côté opposé [BC], et que le bord replié de la feuille vienne couper [DC] au point S. On trace le cercle inscrit dans le triangle rectangle SCQ, il est donc par définition tangent à la fois à ses trois côtés.
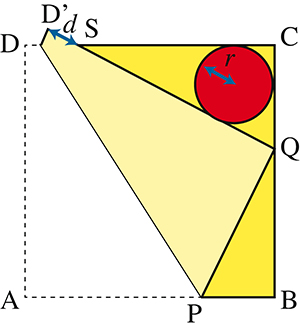
Le but du problème est de comparer le rayon r de ce cercle et la mesure d du segment [D’S] du côté replié qui déborde à l’extérieur de la feuille.
1°) On imagine d’abord que le point Q est au milieu de [BC]. Calculer d et r puis le rapport d / r.
2°) Au lieu d’imaginer que le point Q vérifie BQ = BC / 2, on suppose maintenant que le point Q est tel que BQ = BC / k, avec k un réel strictement supérieur à 1. En faisant varier k, on admet que l’on pourrait avoir alors toutes les positions possibles de Q sur le côté ]BC[.
Calculer d et r en fonction de k, puis le rapport d / r.

