Le courant entre Bêta et l’architecte Tony Desplaques est tellement bien passé dans le numéro 211 de Tangente que ce dernier a accepté de le prendre comme stagiaire au sein de sa structure. La première mission de l’étudiant à l’Institut intergalactique consiste à réaliser une petite pige sur un projet original, commandité par les Adorateurs de Peter Agor (affectueusement surnommé Pete).
Les origines du culte lié à Peter Agor sont passablement obscures, tout comme la contribution supposée de ce dernier à l’existence même de l’Institut intergalactique, mais au fil des siècles, ses adeptes ont acquis un certain pouvoir ainsi que de quoi financer leurs activités ‒ raisonnablement occultes et mystérieuses à souhait. Ils désirent, en l’occurrence, aménager, dans un espace attenant à leur siège, un parterre découpé en cinq zones, dont la forme doit être identique à celle de leur logotype.
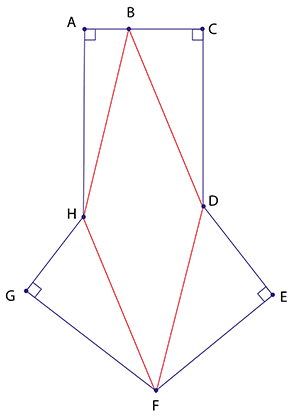
« Voici à quoi ressemble le signe de reconnaissance de la confrérie, indique Tony à Bêta. La section centrale est un losange mais, particularité qui fait le charme du projet, chacun des autres côtés de la forme doit avoir une longueur différente de celle de n’importe quel autre. Les quatre triangles qui encadrent le losange sont rectangles. Une contrainte supplémentaire vient du fait que chaque clôture délimitant une zone est constituée par l’assemblage de barrières de taille identique qu’on ne peut pas découper. Sachant que nous ne pouvons pas réaliser de clôtures droites composées de plus de cent barrières pour des raisons de sécurité, pouvons-nous accepter le projet ? Et si oui, combien de barrières devrons-nous utiliser ? »
Voilà l’énoncé sur lequel planche Bêta, muni d’un papier, d’un crayon et de l’aide bienveillante de sa camarade Epsilon.
Un culte « primitif » avec un heptagone
« Bien, résume Epsilon, nous pouvons utiliser la taille d’une barrière comme unité. Chacun des segments de la forme doit mesurer un certain nombre d’unités entières. Déjà, vois-tu le lien entre ce problème et les triplets pythagoriciens ? »
Et vous, cher lecteur ? Comment reformuleriez-vous la question en faisant appel à cette notion ?
« À présent, poursuit Epsilon, commençons par trouver la liste des triplets primitifs {a, b, c} avec a2 + b2 = c2, dont les composants sont inférieurs à 100. Avec la formule classique, ce n’est pas compliqué : {a = p2 ‒ q2 ; b = 2pq ; c = p2 + q2}, où p > q, p et q premiers entre eux et au moins l’un des deux est pair. »
Trouverez-vous, cher lecteur, les quinze triplets respectant a, b, c inférieurs à 100 ? Comme Bêta, vous pouvez vous aider d’un tableur, qui accélérera les calculs en faisant varier automatiquement les valeurs possibles pour p et q.
« Ok, fait Bêta en examinant les résultats. Je ne trouve pas mon bonheur là-dedans… Il n’y aurait donc pas de solution ? Les adorateurs de Peter Agor vont être déçus…
‒ Attends ! Tu oublies que cette formule ne donne que les triplets primitifs, c’est-à-dire ceux dont les composants n’ont aucun diviseur commun à tous les trois. Si {a, b, c} est un triplet vérifiant a2 + b2 = c2, alors {ka, kb, kc} fonctionne aussi pour tout k entier. Il faut donc encore regarder les triplets qui peuvent être obtenus en appliquant un même coefficient multiplicateur à ceux déjà trouvés, sachant qu’on doit encore une fois se limiter aux valeurs qui restent inférieures à 100. »
À présent, cher lecteur, pouvez-vous dire si le projet est réalisable et si oui combien de barrières devront être utilisées au total ?

