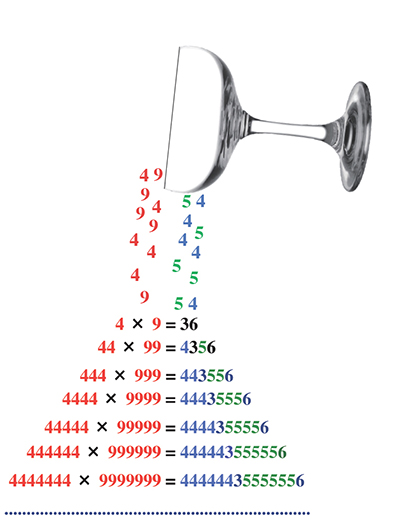
Dans cette cascade numérique, la multiplication par 9…9 produit des motifs répétitifs. Comment l’expliquer ?
À la nième ligne de la cascade, on a :
4…4×9…9=(4×1…1)×9…9=(4×10n−19)×(10n−1)=4×102n9−8×10n9+49.\begin{aligned} 4\ldots 4 \times 9\ldots 9 &= (4 \times 1\ldots 1) \times 9\ldots 9 \\ &= \left(4 \times \frac{10^n-1}{9}\right) \times (10^n-1) \\ &= \frac{4 \times 10^{2n}}{9} - \frac{8 \times 10^n}{9} + \frac{4}{9}. \end{aligned}
Ainsi, pour n = 3, par exemple, on aura, pour résultat :
L’opération a fait « disparaître » la partie décimale des quotients.
Les cascades de ce type se justifient, dans le cas général, par l’égalité suivante :
(k×10n9−k9)×(10n−1)=k×102n9−2k×10n9+k9\left( \frac{k\times 10^n}{9}-\frac{k}{9} \right) \times (10^n-1) = \frac{k\times 10^{2n}}{9} - \frac{2k\times 10^n}{9}+\frac{k}{9}
où k est un entier compris entre 1 et 9 (dans l’exemple précédent, k = 4) et où n, qui représente le numéro de la ligne, désigne un nombre entier naturel non nul.
D’autres multiplications fournissent également d’intéressantes régularités.

Une autre égalité prolifique

Dans cette nouvelle égalité, n est un nombre entier non nul, et a et b peuvent prendre les valeurs 1, 2 ou 3 (la valeur 3 ramenant à l’égalité précédente).
(a×10n3−a3)×(b×10n3−b3)=ab×102n9−2ab×10n9+ab9.\left( \frac{a\times 10^n}{3}-\frac{a}{3} \right)\times \left( \frac{b\times 10^n}{3}-\frac{b}{3} \right) = \frac{ab\times 10^{2n}}{9} - \frac{2ab\times 10^n}{9} + \frac{ab}{9}.
En prenant a = 1 et b = 2, on obtient la cascade suivante :
33...3 × 66...6 = 22...2177...78,
dont le sommet est constitué par l’égalité 3 × 6 = 18,
dont le produit de gauche comprend n chiffres « 3 » et n chiffres « 6 »,
et dont le résultat à droite est composé de n – 1 chiffres « 2 » et n – 1 chiffres « 7 ».
Ainsi, pour n = 3, on obtient :
Trouvez une cascade numérique dont le sommet est constitué par l’égalité 7 × 8 = 56.